傾いた剛体の荷重

*本ページは動画（その18）のための補足資料です。

ある一様に質量が分布した棒状の剛体を両端の二点で支えるとすると、棒が水平の時では両端の荷重は同じになりますが、棒を傾けると下の端の方の荷重が増える例の、理論的な計算です。

良く、御神輿（おみこし）とかでふざけて後ろの人が「うりゃ〜」って高く持ち上げると、前の人が重くなったりしましたよね？（笑）
今回はこの話の解説です。

多くの人は「下が重くなるのは当たり前だ」と思うと思っているのですが、ゲストと同様に「重心の位置が変わらないのになぜ片方に掛かる力が重くなるのか？」といった疑問を持つ人がいるかもしれないので、一応書いておきます。
ま、確かに物理においては定性的な話だけで終わらせるのは良くないですしねっ。
探せばどこかに同様の計算が載っているのかも知れませんが、ちょっと解いてみました。

実際の車では、重心はロール軸やピッチング軸の周りを回転しますが、今回の例では棒は重心の周り、つまり（質量が一様なので）棒の真ん中を回転軸として傾いたものとしてみましょう。（まあ棒は、どこを中心に回転させても傾き角が同じなら変わりませんが）



図1　水平の棒


図1は水平に置いた棒の例です。左右に掛かる荷重は当然同じで、質量がmなので、荷重はmg/2[N]となりますね。

次に図2の様に棒を角度θ だけ傾けてみましょう。


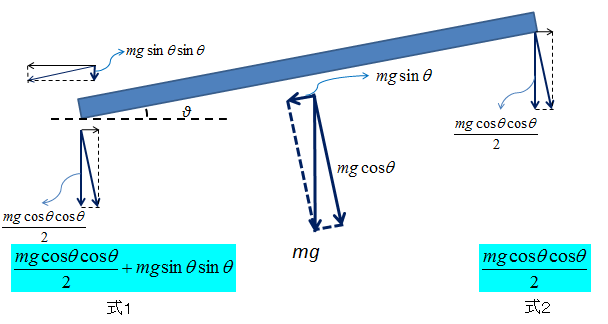
図2　傾いた棒

棒を傾けると、重力は当然棒に対して垂直には掛かりませんね？
常に重力は真下に掛かりますから。
そこで、棒にかかる重力を棒に対して垂直の成分と水平の成分に分けてみましょう。
図2の様に垂直の成分は、mgcosθ、水平の成分はmgsinθ。
垂直の成分は左右で同じだけ分配されるので、両方共mgcosθ/2。
右端を下に押す力は垂直成分だけなので、この力の中から真下に押す、荷重となる成分を抽出すれば良いですね？
つまり、
mgcosθ/2×cosθ
ですね。

一方左端に掛かる力は、右と同様のmgcosθ/2×cosθ の力に、棒の水平成分の力の縦成分を足したものですね？
つまり、mgsinθ×sinθ
を足したものとなりますね。

よって左端を真下に押す力は、
mgcosθ/2×cosθ + mgsinθ×sinθ
となり、右端よりもmgsinθ×sinθ だけ大きくなります。

よって棒を角度θ 傾けると、下の端に掛かる荷重の方が、mgsinθ×sinθ だけ大きくなります。

ちなみにもちろん、両端の荷重を足したものはmgとなります。
式1と式2と足せば、
mg(sin²θ+cos²θ)
で、高校数学で
sin²θ+cos²θ=1
という公式は、よく使うので習ったと思います。
よって両端の荷重を足せば、mgです。

また左右方向については、右側に動かそうとする力も左側に動かそうとする力も
mgsinθcosθ
となって釣り合っていますね？よって当然重力の力で左右に動くことはありません。

また棒を90度、つまり垂直に立ててしまえばsinθ が1、cosθ が0になるので、当然左端に100%の荷重mgが掛かり、右端は0となりますね。

こんな感じです。
ん？当たり前の事を証明するのに意外とめんどくさいって？（笑）
確かにこういうケースでは、身近にある物の実験で説明する方が遥かに楽なんですよね。

ただ物理学は、全ての原因や法則を「数式」を使って説明しなければならない、定量的でなければならない学問だということを、心のどこかに留めておいてもらえればと思います。


Back        Top