強いブレーキとジワッとしたブレーキではどちらが速いのか
さて、ブレーキの踏み方には色んな意見が有りますね。
ガツンと思いっきり踏んだ方が速いと言う人もいれば、ジワーっと丁寧に踏んだ方がいいと言う人もいます。
ブレーパッドなどの効き味についても、初期が強い方がいいとか、初期は弱くて踏むに従って効く方がいいなど、今でも好みが分かれる様ですね。
私は、一番速く走るための、減速のためのブレーキ、つまり止まるのためのブレーキは、「強くて短いブレーキだ」とずっと言ってきましたが、正直今一受け入れない人もいますかね。
それよりも、あまり突っ込みすぎずに手前からジワッとブレーキを効かせて、コーナーに入って行く方が速いと考えている人もいるようです。
まあ、車の世界に有りがちなこれらの不毛な論争?に、一応数学的な答えを書いておこうと思います。
今回は簡単な例として、180Km/hのスピードで直線を走っている車が、入り口で80Km/hまで減速しないと曲がれないコーナーに進入するケースを考えてみます。
ちなみに、80Km/hに減速して曲がり始める位置は同じとします。
さて、それでは2種類の走り方で、どちらが速いのかの実験です。
一つ目の走り方は、コーナーに向かって思いっきり突っ込むイメージで、ギリギリまで180Km/hを維持して、ガツンとブレーキを踏んで一気に速度を落とす運転です。
もう一つの走り方は、それよりも手前からジワッとブレーキを踏んで速度を落として、コーナーに入って行く運転です。
まあ、何となくどっちが速いのか分かると思いますが、ここは物理のページなので、定量的に行ってみましょう。
ちょっと図を書いてみました。 縦方向が速度で、横方向が時間です。
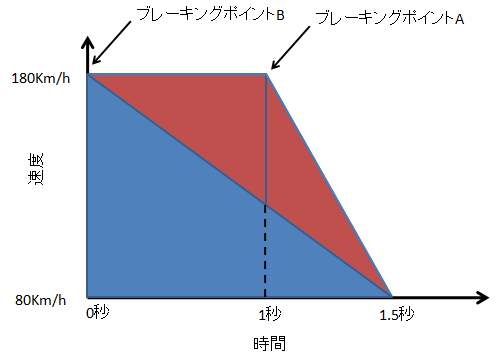
図1 ブレーキの踏み方と進む距離の関係
青い線が、手前からジワッとブレーキを踏んだ場合の、時間と速度の関係です。
徐々に速度が落ちて行って、最後に80Km/hになります。
赤い線が、青い線よりも1秒先まで突っ込んで、ブレーキをガツンと強く踏んだイメージです。
もちろん、これも最後に80Km/hになります。 また、80Km/hになる位置も同じとします。
ちなみに、ジワッとブレーキを踏んだ場合には80Km/hになるのに1.5秒かかるとし、ガツンと踏んだ場合には0.5秒かかるとします。
ブレーキング時間が3倍違うとは極端な気もしますが、実際に初級者と上級者とではこれ位違う物です。
それでは、図1より1.5秒で進む、両車の距離を求めてみましょう。
さて、速度を時間で積分したのが距離でしたね??
この図で言うと、積分ってのは簡単で、三角形の面積が積分した答えその物で、進んだ距離となります。
つまり、青い三角形の面積がジワッとブレーキを踏んだときに、1.5秒で進む距離です。
青い三角形と赤い三角形を足したものが、ガツンとブレーキを踏んだ車が1.5秒で進む距離ですね。
さて、もう解りましたね。
赤い三角形の面積の分だけ、ガツンとブレーキを踏んだ運転の方が、同じ1.5秒で長い距離を走れる訳です。
図を見れば、とても当たり前ですよね。 今までの論争は何だったのか?(笑)ですね。
では実際に、数値を出してみましょうか。
青い三角形の面積は、
1.5秒×(180-80)Km/h / 2 ですね。三角形の面積は、底辺掛ける高さ割る2ですね。
MKS系単位にすると、
1.5秒×(180-80)×1000 /60 /60 [m/s] / 2 = 20.83[m]
ですね。
次に、赤い三角形と青い三角形を足した面積は、1.0秒までは四角で、その先の0.5秒は三角なので、それを足せばいいだけですね。
よって、四角の部分は、
1.0秒×(180-80)Km/h
MKS系単位にすると、
1.0秒×(180-80)×1000 /60 /60 [m/s] = 27.78[m]
三角の部分は、
0.5秒×(180-80)Km/h / 2
MKS系単位にすると、
0.5秒×(180-80)×1000 /60 /60 [m/s] / 2 = 6.94[m]
三角と四角を足すと、
27.78[m] +6.94[m] = 34.72[m]
ですね。 なんか、中学の幾何学を思い出しますねぇ(笑)。
さて、今回は見やすくするために80Km/hをスケールの一番下に持ってきましたが、実際に進む距離は、この面積に80Km/h分の距離を足したものですね。(わかりますよね?)
つまり、
1.5秒×80×1000 /60 /60 [m/s] = 33.33[m]
を上記の面積に足したものが、実際に進む距離となります。
よって、ジワッとブレーキを踏んだ時には、20.83[m]+33.33[m]=54.16[m]。
ガツンと踏んだ時には、34.72[m]+33.33[m]=68.05[m]。
ですね。
つまり、ジワッとブレーキを踏む運転では、54.16[m]進んでいる間に、ガツンとブレーキを踏んむ運転では、68.05[m]進んでいる事になります。 同じ、1.5秒の間にです。
そして、
両車の進む距離の差は、赤い三角形の面積その物ですね。
赤い三角形の面積を求めるのは簡単で、ガツンと踏んだ時の面積から、ジワッとブレーキを踏んだ時の面積を引いたものですね。
つまり、68.05[m]から54.16[m]を引いた物です。
よって赤い三角形の面積は、
68.05[m]− 54.16[m] = 16.89[m]
で、今回の例の場合、ブレーキングだけで16.89[m]もの距離の差が出る事になりますね。
例えば、もしも並走してコーナーに入ると、ジワッと踏んだ方があっさりと、16.89[m]離されてしまうわけです。
ついでにタイムも計算してみると、減速終了時の速度が80Km/hなので、80Km/hでコーナーに進入するとすると、
16.89[m] / 80[Km/h] = 0.76秒
となり、例えばサーキットならば、このコーナーのブレーキングだけで、0.76秒も離される事になります。
(逆にレースなどで追いかけている場合は、16.89[m]、0.76秒を一気に詰められる事になりますね。)
余談ですが、直線で、エンジンパワー(加速力)で、0.76秒縮めようと思ったら大変です。
まして、今回ジワッとブレーキを踏んだ時に使った、54.16[m]しかない直線ではかなり難しいでしょう。
相当馬力の差が有るか、直線が長い必要が有りますね。
しかし、ブレーキングでは短い直線域で、あっさりとこれだけの差が付いてしまう事が有る訳です。
つまり、一番速く走るための減速ブレーキングは、「強くて短いブレーキ」と言う事が、物理的、数学的に明らかですね。
しかし
現実の世界では、タイヤのロックコントロールは難しいし、直線的に速度が落ちるわけではないので、図の線の様に綺麗に減速するのは難しいでしょう。
ですが理論がわかれば、最適解を目指して、いかにそれに近づけるブレーキングが出来るかを実践すれば良いわけです。
減速は加速と違って、ドライバーの技術が占める割合が大きいので、上手いブレーキングを身に付ければ、お金を掛けずに大幅に速くなって、タイムアップもできるはずですね。
以上