距離損とスピード損
さて、久しぶりにちょっと物理っぽい内容の話を書いてみましょう。
スポーツ走行に興味のある人ならば、恐らくこれらの言葉を聞いたことが有るでしょう。
「アウト・イン・アウトライン」。 「スローイン、ファストアウト」。
これはコーナーの走り方を表したものですが、
これらはスポーツ走行の基礎で、速く走るためには今や鉄則となっているものですかね。
でもこれらは本当に速いのでしょうか? もっと言えば、最適解なのでしょうか?
具体的に計算して、論理的に正しいと証明した人は居るんでしょうか?
まあ恐らく居るのだと思いますが、私はその厳密な解説を見た事がないので、ちょっと書いてみようと思います。
まずはじめに覚えておくことは、「車は直線が一番速い」という事です。 ま、当たり前ですね。
直線では横Gが発生しないので、タイヤの横グリップは一切使いません。
つまり摩擦円の縦のグリップを、全て加速に使えるからです。
またラインについても同様です。例えばA地点からB地点まで移動するとしましょう。
一番距離が短いのは、A地点とB地点を結ぶ直線です。 というか、直線の定義自体が「2点の最短距離を結ぶ線」なので、当たり前ですね。(一応書いておきますが、ユークリッド幾何学に於いて、とします。わからない人は無視してください。)
つまり、最も速いスピードで、最も短い距離を走れるわけですから、この直線のケースは簡単ですね。
直線をわざわざ真っすぐに走らずに、グネグネと曲がったほうが速いと思う人はいないでしょう(笑)。
ところがこの世界にコーナーがある限り、常にまっすぐはに走れません。 それでも出来るだけ、「直線に近付けて走ろう」、というのがアウト・イン・アウトラインです。
正確に言うならば、出来るだけ大きい円を描くように走ろう、と言うものですね。 円の半径が無限大になれば、ラインは直線になるので、出来るだけ大きな半径(良くR(アール)と呼ばれるもの)の円を走ろうというものです。
そのためには、外側ギリギリからコーナーに入り、イン側ギリギリを通って、また外側ギリギリを目指して脱出する必要が有るわけです。ま、図を書いて見れば明らかですね。
半径(R)が大きければ、何度も書いた式、
遠心力 F = mV2
/ R
より、遠心力は小さくなります。
よって、アウト・イン・アウトラインは遠心力が小さいので高いスピードを維持してコーナーを抜けられる、といった感じでしょう。
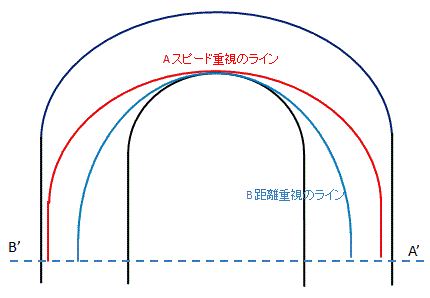
図1
アウト・イン・アウトライン
まあ、一般にこういった説明が多いと思いますし、逆にこれ以上の説明を私は見た事が有りませんかね。
しかしこのラインには、ひとつ考慮しなくてはいけない重要な事が有ります。
それは、「アウト・イン・アウトラインは遠回りをしている」、という事です。
図1を見てみてください。 イン側を通るラインBと比べて、明らかに半径(以下Rとします)が大きい事はわかりますが、ラインBと比べて遠回り、つまり長い距離を走っていることも明らかですね。
時間(図ならA'からB'までの区間タイム)というのは、距離÷速さ ですから、いくらスピードが速くても長い距離を走っている事はロスとなるのです。 この距離のロスの事を、「距離損」と言うことにします。
逆に、イン側の近道をするラインは距離は近いですが、Rが小さいため、遠心力が大きく、高いスピードでは曲がれません。
よって、ラインAよりもスピードを落とす必要があります。
このスピードのロスを、「スピード損」と言うことにします。
ちなみにモータースポーツの世界では、多くの場合には、距離損よりもスピード損を優先するようですね。
つまり、Aのアウト・イン・アウトラインの方を取ることになっているようです。
それでは実際には、どっちが速いのだろうか?という疑問の前に、久しぶりに一つ出題してみます。
もしも、このコーナーの区間A’〜B’のタイムが、ラインAとラインBで全く同じだったとしましょうか。
つまり、距離のロスと、スピードのロスが互いに相殺しあい、偶然同じタイムになったとします。
そして、このコーナーが例えばサーキットの中の一つのコーナーだったとしましょうか。
また、仮に他の部分の走り方は全く同じで、タイムも同じだったとしましょう。
するとどっちのラインの方が、サーキット一周のタイムが速いでしょうか?
とても簡単な問題ですが、以外と瞬時に答えられなかった人が多いのではないでしょうか??
(瞬時に分かった人は、後は飛ばして下さい(笑))
一応解答ですが、答えはAのラインです。
え?区間タイムが全く同じなのに?と思った人もいますかね。
出題を良く見てくださいね。「サーキット一周のタイム」です。
ではラインAとラインBでは、何が違うのでしょうか。
通る道、それこそラインが違うのはもちろんですが、コーナー区間が終わるB’の位置でのスピードが違いますね?
例えば、Aのラインでは80Km/hなのが、Bのラインでは、70Km/hだったりするはずです。
ラインAはスピード損を抑えた走りなわけですから。
よって、コーナーの出口で10Km/hも違えば、その先であっという間にラインAの車が先に進みますね?
出口=次のブレーキングポイントでもない限り、一度開いたこの差は縮まる事もひっくり返る事もありません。
今回は区間タイムは全く同じとしましたが、出口でのスピードの差が大きいのならば、距離損を抑えたBのラインの方が区間タイムが速くても、Aのラインの方がトータルでは速くなる事が多いでしょう。
よって、コーナーを走るには距離損よりもスピード損を抑える走りをした方が、一般に速いケースが多いと言われているのでしょうし、実際に区間タイムがそれほど大きく違わなければ、やはりスピード損を抑える走りが有効だと私も思います。
ただ、そうはならないケースも有ります。
バトルは除くとしても、例えば、コーナーの出口から近いところにコントロールラインが有るコースで、タイムアタックをする場合等は、もうちょっと事情は複雑です。
と、書いてきたところで、、、続きが聞きたいですか??(笑)
ちょっと新しい事を書き始めたので、読者の方からの反応を待ってみたいと思います。
何となく、誰でも知っている事をダラダラと書いている気がしてきましたので…。
要望が多ければ、このあたりの話をもうちょっと書いてみようと思います。
私はこのライン関係の話を、「コーナリングの幾何学」と呼んでいるのですが、とても数学的に簡単なのに、意外と実行していない人が多い気がするんですよね。