摩擦円を物理する
さて、タイヤのグリップを最大に出すにはに書いた、タイヤのグリップの限界を見るために、良く「摩擦円」(Friction Circle)と言う概念を使用した説明を見ると思います。
下図の様な物ですね。
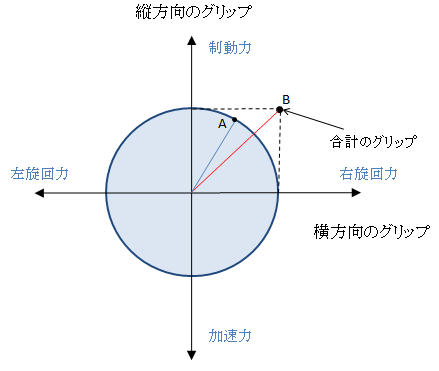
図1 摩擦円の概念
これは、タイヤのグリップ(摩擦力)は縦方向と横方向の合計であり、タイヤに掛かる力は、点Aの様に円の中に入っていなければならず、点Bの様に円の外に出てしまう力が掛かると、タイヤはグリップの限界を超えて滑り出す、という話ですね。この説明は、まあ、何となく説得力が有るような気もしますけど、ちょっと定量的ではないですね。
なぜ点Bでは、タイヤは滑りだすのか、少し物理的に考えてみましょう。
それでは、タイヤのグリップを最大に出すにはに書いた通り、実際にタイヤのゴムに掛かる力を考えてみましょう。
ここでは、1200Kg の車重の車を例とし、4輪に同じ荷重が掛かるとします。
すると、1輪当たり300Kgですね。
今回は この1輪だけをクローズアップして、考えてみましょう。
でわこのタイヤを、強い糸で引っ張ってみるとします。
下図の様なイメージになりますね。
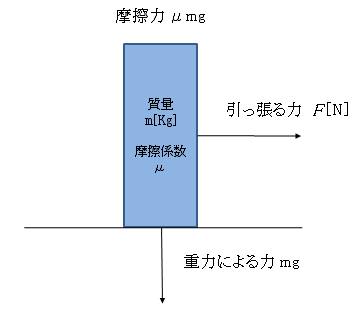
図2 タイヤを前から見た図 ここで、タイヤを滑らせるのに必要な力を計算してみると、
F = μmg
なので、μ を路面とタイヤの平均の摩擦係数0.9とすると、mは300Kg、gは9.8m/s2なので、
F = 0.9×300×9.8 = 2646[N]
となりますね。
これが、このタイヤの静止摩擦力です。
これは実際の車の例で言うと、ブレーキでロックする寸前や、スライドする寸前の最大の摩擦力ですね。
つまり、このタイヤを滑らせるためには、2646[N](=270[Kgf])以上の力で引っ張る必要が有るわけです。
次に、図1の摩擦円の点Bを考えてみましょう。
この点は摩擦円の外にあり、縦方向、横方向ともに、タイヤの最大の摩擦力、2646[N]ですね。
では今度は、それぞれ縦に2646[N]、横に2646[N]の力で引っ張ってみましょう。
タイヤを上から見ると、図の様になります。
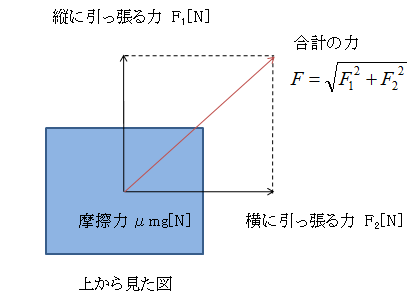
図3 タイヤの接地面を上から見た図
縦、横それぞれの引っ張る力はベクトル量なので、両方の力を足したものが合計のタイヤを引っ張る力ですね。よって、ベクトルの和となります。
そのベクトルの和は赤線のベクトルとなります。
ではこの赤いベクトルの大きさを計算してみましょう。
簡単ですね。長さを求めるには、三平方の定理を使うだけです。
よって図3の合計の力の式より、赤いベクトルの長さ、つまり合計の力は、
F = √(26462+26462) = 3742.0[N]
ですね。
つまりこれは、図2で計算した静止摩擦力である、2646[N]よりも1096[N]も大きくなり、タイヤが滑りだす摩擦力を大きく上回る事になります。
これが、摩擦円の外に出るような力を与えると、タイヤが滑る理由でしょう。
よってこのタイヤには、いかなる時も合計で2646[N]以上の力が掛からないようにしないと、タイヤが滑りだすわけです。
今回の例では、摩擦円の円の半径は、2646[N]だと理解すればよいでしょう。
このタイヤのグリップを説明するための、「摩擦円」と言う概念は、分かりやすい物ですね。
ちなみに、実際の車ではこの摩擦円の大きさ、つまり円の半径は、荷重移動により変化します。
何度も書きますが、摩擦力は、
F = μmg
なので、荷重であるmが変化すれば、当然摩擦力も変化します。
厳密には、タイヤを太くすると何故グリップが上がるのかに書いた通り、μ も変化しますね。
走行中の摩擦円のイメージを図にしてみると、下図の様になります。
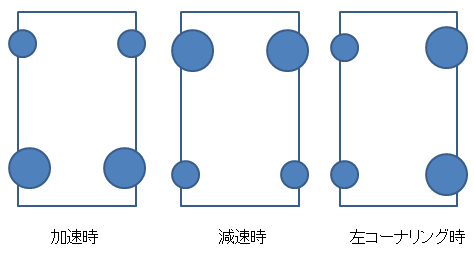
図4 荷重と摩擦円の変化
図4の円の大きさが、それぞれのタイヤの摩擦円の大きさです。このようにタイヤの摩擦円の大きさは、走行中にはダイナミック(動的)に変化している事になりますね。 しかし、この摩擦円を使用した説明は良く出来ていますが、ちょっと疑問を持ちませんか??
新たな領域に行くために、ちょっと考えてみてください(笑)。
続く・・・