ロールと荷重移動と横G その1
さて、せっかく自動車を物理するページなので、そろそろもう一発上の領域に行ってみましょうか。
ロールと荷重移動の話は、色んな所で、色んな形で語られていますね。
例えばー、
車高を下げるとロールが減るとか、はたまた車によっては逆に増えるだとかー。
バネを固めるとロールが減るけど荷重移動量は変わらないとか、変わるとかー。
足は固い方がスポーティーだとか、限界が高いだとかー。
トレッドを広げると限界コーナリング速度が変わるとかー。
重心は低い方がコーナリング限界速度が高いだとかー。
車高を下げると、ロールセンターを補正しないと逆に限界が下がるだとかー。
雨の日はバネレートや減衰力を下げた方がコーナリングが速いとかー。
エトセトラ。
ま、経験則や怪しい理論等の色んな話があふれていますが、ここではちょっと物理の目で見てみましょう。
まずロールとは何でしょうか? ちなみに、Wikipediaで調べてみると、
「ローリング (rolling) は、乗り物など前後・左右・上下が決まった物体が、前後を軸(X軸)として回転(あるいは傾斜)すること。ロール (roll) とも。」
だそうです。
他に車体に働く運動は、前後方向に回転運動をするピッチングと、曲がる時などに地面に対して水平に回転するヨーイングが有りますね。
まあピッチングとヨーイングについてはまた書くとして、重要な事はロールを含めこれら運動は回転運動、つまり円運動だと言う事です。
簡単に言うと、車では横Gが掛かった時に、重心が真横に移動する事は有りません。
もしも真横だったら、外側のバネは縮みませんね?
まあ、タイヤが滑れば真横に移動しますが、今回は滑らない場合についての話にします。
ロールする時に重心は、有る軸を中心とした円運動をします。
この軸の事を「ロール軸」と言ったり、はたまた、ロール軸の断面である「ロールセンター」と言ったりしますね。
しかし、この円運動をする事が、色んな事を非常に複雑にしています。
更には、車においては円運動の中心、つまり回転軸であるロール軸自体が動いてしまう事が有るので更に複雑になりますが、ここでは取りあえずロール軸は動かないとします。
そして円運動をする重心についてですが、これまた計算においては「車の質量はこの点に集まっていると考えて良い」、と言う場所(点)の事ですねぇ。
物理だと、どうしてもこういう抽象的な概念が出てきます。
実際には、重心が有る場所は車によっては室内の空っぽの空間のどこかかもしれません。
それでも、そこに車の質量が全て有ると考えて良い事になります。
このように物理学では色んな事を近似している事は覚えておいてください。
それでも現在、最も現象を正確にあらわせる道具が物理学でしょう。
さて、ちょっと話が固くなったので本題に入りましょう。
ロールが重心の回転運動、円運動であると言う事は、重心を回転させる力が何か働いている事になります。
この力こそが、加速度、一般に言う「G(ジー)」です。
今回はロールの話なので、横方向の加速度、つまり「横G」ですね。
車がコーナリングすると、重心に遠心力が働きこれが横Gになる訳です。
この力が、ロールモーメントとなり、重心がロール軸の周りに円運動をさせる力となります。
ロールモーメントとは、とても簡単な言葉で言うと「回転させる力」の事です。
別の言葉だと、トルクが同意です。 詳しくは、自動車に必要な物理学 を見て下さいね。
つまり、「遠心力で重心が真横にGを受けるが、タイヤが滑らないためロール軸の周りに円運動をする。」
これがロールの正体です。
そしてトルク(力のモーメント)とは、回転軸と力が掛かる点(この場合は重心)との距離と、力を掛けたものでしたね?
正確には、両方のベクトルの外積です。
つまり車をロールさせるトルクは、ロール軸と重心との間の距離と、重心に掛かる横Gを掛けた物です。
よって、ロール軸と重心の距離が大きければ大きい程ロールさせるトルクは大きくなり、横Gが大きければ大きい程ロールさせるトルクは大きくなりますね。
それでは分かりやすい様にちょっとシンプルなモデルを作ってみました。
図1を見てみて下さい。
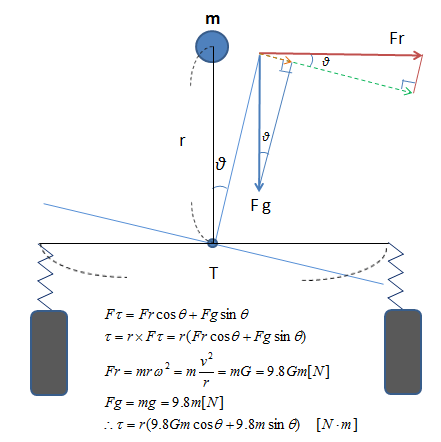
図1 ロールのモデル
図1は非常にシンプルなモデルです。 アームも有りませんしね。
フレームに直にバネが付いていて、その下に直にタイヤが付いています。
実際の車はもう少し複雑ですが、足廻りの構造などは車によりまちまちですし、正確にモデルを作るのは大変なので、このようなシンプルなモデルで考えてみます。
ただこれは、基本的に実物の車をほぼ再現出来るモデルだと思います。
それでは図1のモデルを具体的に説明してみましょう。 車を後ろから見た図だと思って下さい。
まず、上の青い丸が車の「重心」です。
つまり、車の質量は全てここに集まっているとして計算する点です。 ここで車の質量は、mとします。
次に、下の青い丸が、ロール軸の断面です。 ロールセンターとも言いますね。
そして、ロールセンターと重心の距離をrとします。
次に、右のタイヤと左のタイヤの距離をTとします。 これはトレッドですね。
以後の計算では、この車に遠心力(横G)が掛かるとします。
遠心力による、横Gの力を、赤ベクトルのFrとします。これは、水平方向の力です。
そして、重心を引っ張る重力の力を、青ベクトルのFgとします。これは、垂直方向の力です。
また、車がロールした時のロール角をθとします。
それではこのモデルで、重心をロールさせる力(トルク)を求めてみましょう。
ここで大事な事は、車をロールさせるトルクは、図1の様に横Gと重力の力を合わせた物になると言う事です。
自動車に必要な物理学より、
トルクは回転軸と力を入れる点の距離のベクトルと、力のベクトルの外積でしたね?
つまりここでは、ロールセンターと重心との距離と、重心に掛かる回転に対する水平の力成分(図の緑のベクトル)を掛けた物です。
ロールをさせる力に横G以外に、重力が入っているのが意外かな?
図1よりロール角が0度でない限り、必ず重力もロールさせる力となる事になりますね。
この現象を分かりやすく言うなら、例えば車高調正式サスペンションで、右だけ車高を下げると車体が傾き、重心が右に移動して、より右のバネを縮める力となりますよね?
だから例えば、全長調整式の車高調で右の車高だけ5mm下がる様に調整してジャッキから降ろすと、不思議な事に実際の車高は5mm以上下がる訳です。逆に左は全く変えて無いのに上がりますね。
これは、横Gの力で車がロールすると、重力の力で更にロールが増えるのと同じ現象です。
それでは具体的に、ロールさせるトルクを計算してみましょうか。
何か高校物理の試験問題を思い出しますね(笑)。
まず車を回転させる方向の力を求めてみましょう。 これは図1の緑のベクトルですね。
これをFτとして、ロール角をθとすると、
![]() ・・・式1
・・・式1
となりますね。
ま、図1を見れば簡単です。
次に実際のトルクは、rとFτのベクトルの外積なので、
![]() ・・・式2
・・・式2
となりますね。
ま、Fτは水平の力だけにしてありますから、スカラー量として距離rと掛けるだけですね。
そして、Frは遠心力なので、
![]() ・・・式3
・・・式3
Fgは重力なので、
![]() ・・・式4
・・・式4
となりますね。
よって式2に、式3と式4をそれぞれ代入すると、重心をロールさせるトルクは、
![]() ・・・式5
・・・式5
となりますね。 まあ簡単ですね?
この式5のGが横G、θがロール角です。
つまりロールさせるトルクは、車重と横Gとロール角と、ロールセンターから重心までの距離で決まる事になりますね。
そしてこの式より、ロール角が大きくなるほど、ロールさせる力は横Gよりも重力が支配的になる事が判ると思います。
極端な例だと、式5より、横Gが1Gの時に45度ロールしていれば、ロールさせる力の半分は横Gで、もう半分は重力と言う事になりますね。
そしてそこから先のロールは、重力の力の方が支配的になる事になります。
まあこの話は、後で詳しく書きます。
ちょっと長くなったので、次回に続く・・・。