タイヤのグリップを最大に出すには
さて、突然ですが米粒一つと、1000Kgの鉄の塊が無重力の宇宙空間に浮いていたとします。
例えばスペースシャトルの中でもいいです。
この時に、止まっている米粒を動かすのに必要な力と、止まっている1000Kg、つまり1トンの鉄の塊を動かすのに必要な力はどちらが大きいでしょう?
答えは、両方とも同じです。 その力とは、「0よりも大きい力」です。
いいですよね? 自動車に必要な物理学の「力とは」の項を読めば解ると思います。
勿論同じ力を与えた時の、米粒と鉄の塊の速度は異なります。
ただ、静止している物を動かすのには、質量に関係なく、0ではない力が有ればいいのです。
一応式を書いておくと、力とは、
F=ma
でしたね?
と言う事は、質量mを持つ物体が得られる加速度は、
a=F/m
ですから、Fが0でなければ、加速度aは0にはなりません。
つまりたとえ非常にゆっくりでも、物体は動き出すわけです。
これ、結構勘違いしている人がいるようなので、一応書いておきました。
さて 次に、地球の地面で同じ実験をしてみましょう。
地面に置いた、静止している米粒と、1000Kgの鉄の塊が有るとしましょう。
これを動かすのに必要な力はどちらが大きいでしょうか??
経験的にも、もちろん鉄の塊の方が遥かに大きな力が必要だと分かりますね。
では宇宙空間と、地上とでは何が違うのか?
それは唯一、「摩擦力が有るか無いか」です。
この摩擦の有無が、唯一の違いですね。
地面に置かれている質量の有る物体には、必ず摩擦力が生じます。
例の、
F=μmg
って奴です。
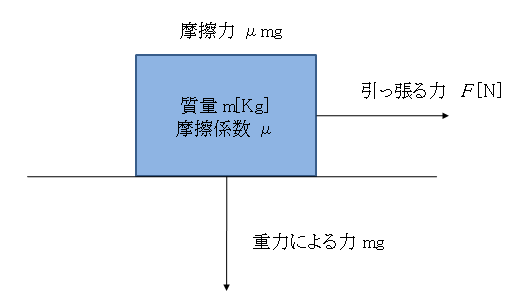
図1 地面の摩擦力
つまり、このFを超える力を与えないと、静止している物体は動き出さない訳ですね。この物体が「止まっている時」の摩擦力が非常に重要で、物体は止まっている時に最大の摩擦力を発生します。
この時のμを、静止摩擦係数と言います。
静止摩擦係数は、一般に最大摩擦係数になります。
これも経験的に分かると思います。
レッカーを引っ張る時でも、重い荷物を引きずる時でも、一番力が必要なのは、止まっているのを動かす瞬間だと思います。
一度動き出してしまえば、それほど力を掛けなくても動かし続けたり、加速させる事が出来るはずです。
ちなみに、この動き始めた後の摩擦係数を、動摩擦係数と言います。
もしも 目の前にコップが有れば、ちょっと実験してみてください。
止まっているコップを動かす力と、動き始めたコップを動かし続ける力は違うと思います。
これが、静止摩擦係数が最大の摩擦係数だという証拠です。
これは、人生に似ています(笑)。
スポーツにしろ、勉強にしろ、仕事にしろ、何もしていない状態から始める時が一番エネルギーが必要ですよね?
でも一度始めてしまえば、意外と思ったよりも楽に出来てしまう物です。
何やら考えさせられる物理法則ですねぇ。
さて、今度は肝心のタイヤで考えてみましょう。
もちろんこの法則は、タイヤでも全く同じです。
タイヤにロープを付けて、体で引っ張るトレーニングなんて今は無いのかもしれませんが(笑)、あれも止まっているタイヤを動かす瞬間が一番力が必要で、大変です。
そして、 車にタイヤを取り付けた場合も全く同じです。
タイヤが最大の摩擦力、つまりグリップを発生するのは、タイヤが止まっている時です。
逆に、タイヤが滑りだすと摩擦力は一気に下がります。
これは、例えばブレーキをロックさせると制動距離が伸びるし、ハイパワー車でアクセルを雑に踏んでホイールスピンさせると、摩擦力が下がり、タイヤがその場で空転して前に進まないなど、車の世界では当たり前の現象ですね。
つまり、車のタイヤに最大のグリップを発生させるには、タイヤを制止させ、滑せない事となりますね。
ただ ここで、次のような疑問が出てくると思います。
それは、
「では転がっているタイヤは、止まっているのか、滑っているのか?」
転がるのと、滑るのとでは全く現象が違います。
直線を転がっているタイヤは、静止していると考えればオッケーです。
転がることでタイヤの接地面がコロコロ変わるだけで、滑っているように見えても、タイヤの接地面自体は滑っていません。
(厳密に言えば、アライメントのトー角などが付いていれば、滑っている事になりますが、ここでは無視します。)
ただし、ハンドルを切って曲がる時には微妙に滑っている事になりますが、その話はちょっと難しいので、ここではカットします。
さて、 と言う事は、タイヤの最大グリップを出すためには、静止摩擦係数を出せばいいわけで、タイヤを一切滑らせなければいい事になりますね。
続く…