車重と荷重とグリップの関係

さて、答えは出ましたか？（笑）
実は半分は、もう書いてしまっているんですよね。

タイヤの銘柄もサイズも同じで、タイヤのグリップの限界を上げるには、どうしたらいいのか。
ちなみに、ここでのグリップ限界とは、タイヤが滑りだす限界域を指すことにします。
さて、もう一度第一部で書いた図を書いてみます。

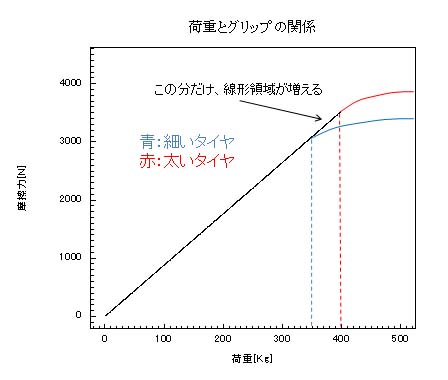
第一部より、図のグリップの線形領域を使えば、タイヤの太さはグリップ力に関係なかったですね。
と言うことは、タイヤの太さを変えないのならば、荷重が線形領域に常に収まるようにする方法を考えればいいだけです。
線形領域に収めるには、図の通り荷重が小さければ小さいほど収まりやすいですね。
と言うことは、「荷重をいかに小さくすればいいか」を考えればいい事になります。
荷重を小さくするのは簡単です。

一番先に思いつくのは、
「車重を軽くすること」
ですね。

そうすれば、当然荷重も小さくなります。
ちょっと図の例で定量的に考えてみましょう。
細いタイヤは、350Kgまでは線形でしたね。と言うことは、一つのタイヤにかかる荷重が、4つのどのタイヤでも、いかなる時も350Kg以下ならばオッケーな訳です。
もしも車重が350Kgの車ならば、100％オッケーですね。荷重は車重を超えませんから。
しかしながら、実際には、荷重移動で一輪に全ての車重が乗ることは有りません。
仮にフルブレーキで、フロントタイヤに全車重が乗ったとしても2輪で受け持つので、
350Kg×2＝700Kg　なので、車重が700Kgの車でも大丈夫ですね。

しかし、全車重がフロントだけや、リアだけに乗る事も考えにくいですね。
コーナリング中だったら、外側の2輪だけに乗ることも考えにくいです。スタントの2輪走行でもやれば別ですが（笑）。
具体的に、何キロの荷重が移動するかは車によって変わると思いますが、車重を軽くすることは、タイヤのグリップ限界を上げる最も効果的な方法の一つです。

そして、次にもう一つの解です。
それは、
「荷重移動を少なくすること」
ですね。

まあこれは、第一部と重複しますが、荷重移動が少なければ、どのタイヤも図の線形領域から外れることはなく、常に荷重は一定近くで、最大グリップを発揮できることになります。
車のタイヤのグリップ力とは、あくまで4輪全ての合計ですから。

例えば、静止状態で4本全てのタイヤに300Kgの荷重が乗っている、1200Kgの車があったとしましょう。
するとグリップの総量は、
F=μmg [N]　より、
F=μ×300Kg×g ×4本＝0.9×300×9.8×4　[N]
ですね。

この車に、図の細いタイヤが付いていたとすると、荷重移動が起きても1つのタイヤも350Kgを超えることが無ければ、グリップの総合量は変わらないはずです。
あるタイヤの荷重が増えた分だけ、どこかのタイヤの荷重が減っているはずですから。
何度も言いますが、車重は常に変わらないので。

ただ、一つのタイヤでも荷重が350Kgを超えた瞬間に、グリップの総合量が小さくなります。
つまり、
F=0.9×300×9.8×4　[N]
よりも、総合量が小さい値になるわけです。いいですよね？
350Kgを超えたタイヤだけμが0.9より小さくなってしまうからです。
よって、この車の場合、「荷重移動でどのタイヤも、いかなる時も350Kgを超えないようにする。」
これが、もう一つの解です。

具体的に荷重移動を減らすには、ロールやピッチングを減らせばいいわけですね。
これは、車の重心を下げたり、ロールセンターを変えたり、足回りを固めたりと、多くの人が体感しているものですね。
図で言うと、荷重変化を全く起こさせず、全部のタイヤの荷重が常に350Kg以下であれば、タイヤの太さを変えなくても、4つのタイヤのグリップを最大限に発揮できることになりますね。
これは実際に、コーナリングや、ブレーキングでは有効です。（トラクションについては、後述）

さて、答えは当たってましたか？？

ここで少し、軽量化とグリップの話を説明してみましょう。
これは、誤解している人が多いかもしれないので。

良く「軽量化するとグリップが下がる」何ていいますけど、それは嘘っぽいけど本当です。
車重を軽くすると、グリップ、つまり摩擦力自体は下がります。
もう一度書きますが、
F=μmg [N]　
ですから。

車重、つまりmが小さくなるので、摩擦力Fも小さくなります。
これは、グリップ力が下がっていると言って良いですね。
しかしながら、現実の世界ではグリップ限界は上がります。

例えば、ある半径を持つ円周上をグリップ走行で、少しずつ加速しながら走行していたとしましょう。
ちょっと図を書いてみます。

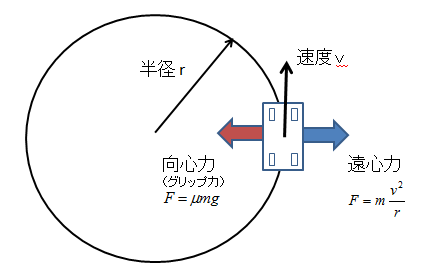
この場合、ある速度で遠心力に負けてタイヤが外に滑りだすはずですが、その速度は、タイヤが同じならば軽い車の方が高い速度になります。
これは何となく、経験的、もしくは感覚的に解りますよね。

さて、それでは物理学的には何故でしょうか？？
第一部を理解した人は、答えが分かっちゃったかもしれませんが、説明してみましょう。

この話で、非常に重要なことは、高校で習う物理学には、理論と実際に起きることが微妙にズレる物と、全く理論通りになる物があるということです。
タイヤの、荷重とグリップ（摩擦力）の関係は、第一部で説明した通り、実際にはある所から理論とズレる例ですね。
サスペンション編に書く予定ですが、バネの力学もある所から理論と実際に起きる現象がズレる例です。
しかしながら、運動の力学は、理論と実際に起きることが完全に一致します。
ここに落とし穴があるわけですね。

ここで、自動車に必要な物理学に書いた、円運動の力学を思い出してみましょう。
遠心力は、
F=mrω²　でしたね。
ωは角速度で、ちょっと分かりにくいので、スピードに変換すると、
スピード v = rω なので、
F=mv²/r

となりますね。
これより、遠心力は速度の2乗に比例することが分かります。
遠心力は、タイヤのグリップのようにある所から式から外れることはなく、どの領域でも実際に、この式の通りになります。
タイヤが滑らないとは、遠心力とそれに対抗するタイヤのグリップ力、つまり向心力が釣り合っているということです。
つまり、
F=μmg ＝mv²/r
が成り立っていると言うことですね。

さて。ここで、少しずつ速度を上げていきましょう。そうすると、
μmg ＜mv²/r
となる速度に達した時に、タイヤのグリップが限界を迎え、遠心力に耐えられずに外に滑り出すわけです。
この式より、μが大きいほど、その限界速度は大きいことになりますね。
物理学では変わらないはずのμは、現実世界ではタイヤに荷重が掛かり過ぎると小さい方向に変化するので、出来るだけμを大きい状態のまま保ちたいわけです。

例えば1200Kgの車重を2倍にすれば、物理理論上はグリップ力も2倍になるはずですが、実際の世界ではそうはなりません。
重くなればなるほど、μが線形領域から外れ、小さくなってしまいますから。
それに対し、車重を2倍にすれば、遠心力はキッチリ2倍になります。
これが、運動の力学はいかなる時も物理の理論通りになるという意味です。

よって、車重を重くすることによるグリップアップよりも、重さによる遠心力の増加の方が勝ってしまう訳です。
そのために、グリップ限界を上げるには、重さによるグリップアップよりも車重の軽さの優位性の方が勝るので、車重を減らした方がいいわけです。

さて、ちょっと難しかったですか？？（笑）
でもこれは、是非理解してほしいところですね。
タイヤのサイズアップをせずとも、グリップ限界を上げる方法はあるのです。
第一部に書いた通り、サイズアップはデメリットも多いので、これらをやった後のステップだと思います。
さて、次に三つ目の解です。これは、第一部の話とはちょっと方向が違う解ですかね。
タイヤは荷重をかけるほどグリップが上がるのでしたね。
しかしながら、上記のように車重を重くして荷重を掛けると、車重増による遠心力等の慣性の増加の方が勝ってしまうため、軽さの優位性が勝るわけでした。

と言うことは、、、一番いいのは、車重は変わらずに、タイヤの荷重だけ増えればいいんですね。
そんな夢のようなことは一見不可能そうですが、それを唯一可能にするのが、空力によるダウンフォースです。
ダウンフォースをかけてやれば、上記の円運動の例で言えば、
μmg ＝mv²/r
の、右のmは車重なので変わらず、左のmだけがダウンフォースで増えることになります。
つまり遠心力は軽い車のままで、グリップは重い車並みです。
正においしいとこ取りで、素晴らしい！！

μが非線形領域に入り、0.9より小さくなろうが関係ありません。
μが小さくなって来ようが、車重が変わらないのならば、荷重を掛けるほどグリップ限界は上がります。
F1等のフォーミュラカーが、車重は600Kgしかないのにタイヤがあんなに太いのは、ダウンフォースにより、タイヤに掛かる荷重が半端じゃないからです。
ちなみにF1 だと最大で大体2トン位のダウンフォースがかかるそうです。
車重が600Kgなので、合わせて2600Kgです！！
つまり、車重が2600Kgの車と同じ荷重がタイヤに掛かっている訳ですね。

そんなに重い車だったら、太いタイヤにしないと第一部で書いた線形領域に収まらないでしょう。
細いタイヤだと、すぐに線形領域を外れ、荷重をかけてもリニアにグリップが上がらない領域に入ってしまいますから。
だから、車重が軽いにもかかわらず、あんなにタイヤが太いんですね。

パワーがあるから太いんじゃないですよ。荷重がかかるから太いんです。
時々パワーがあるからタイヤを太くすると思っている人がいますが、いくらタイヤを太くしても、荷重がかからなければトラクションはかからずに、ホイールスピンするだけです。
大きな荷重をかけらなければ、太いタイヤでも細いタイヤでも全く同じです。

さて、とりあえず以上の三つの答えを用意しましたが、当たっていましたか？？
普段から、物理的な考え方が出来ていれば、それほど難しくありませんね。

実際に、この三つを全て行えば、一番タイヤのグリップ限界を上げられる事は、簡単に予想できますね。
つまり、「車を軽くして、ロールやピッチングを減らして、ダウンフォースをかける…」。
って、これは、レーシングカーがやっている事その物ですね。
これらは感覚的に当たり前だと思っていた物ですが、ちゃんと物理的に考えても、これらはタイヤのグリップ限界を高めるために、実に理にかなっていますね。

余談ですが、F1だけでなく、最近のレーシングカーは、もっぱら空力で性能が決まると言われています。
レーシングカーはコーナーで踏めば踏むほど（速度が上がるほど）車体が安定するそうですが、これはダウンフォース増加により、タイヤのグリップ力が、速度が上がるほど上がるからでしょう。
そして速度アップによる遠心力の増加よりも、ダウンフォースアップによるグリップ増加の方が上回る領域があるため、このようになることがあるのだと思われます。
（特に高速コーナー。もちろん、遠心力とダウンフォースによるグリップアップのどっちが勝るかは、コーナーによって変わります。具体的には、コーナーのrによって変わりますね。遠心力はmv²/rなのでrで変わりますが、ダウンフォースはrは関係なく、スピードだけで決まりますから。つまり、rが大きいほど、同じスピードならダウンフォースの優位性が出るということですね。）

ただしコーナーで遠心力で吹っ飛びそうなので、更にアクセルを踏み込むと言うのは、人間の感覚とは逆のことなので、慣れるまでは怖いそうです。（某プロレーシングドライバー談）。

空力と言えば、ちょっとまた余談ですが、ジャンボジェット機が着陸する時に、どうやって重い機体を止めてるか知ってますか？？
逆噴射？？　勿論、それも有りますが、強烈にダウンフォースをかけてタイヤに荷重をかけているんです。
上下方向の空力は、飛行機は得意ですからねぇ。
だから実は飛行機も、タイヤに荷重をかけてブレーキで止めてたりするんです。
始めにタイヤに窒素を入れ始めたのも飛行機だし、飛行機でもいかにタイヤが重要な役割を果たしているか判りますねー。
　

さて、とりあえずタイヤの太さと荷重とグリップの話はこの辺にしておきます。
いかがでしたか？（笑）

たかがタイヤ、されどタイヤ。奥が深いですねー。
タイヤを知らずして、上手いドライビングなどあり得ないですね。
逆に言えば、タイヤを制すればドライビングの半分は制することができる、と思います。
始めに書いたように、車の性能を出すとは、「タイヤの性能とエンジンの性能を出すこと」ですから。

とりあえず、以上

Back Top