タイヤを太くすると何故グリップが上がるのか
さて、ちょっとエンジンの話が続いたので、トップページに書いたように、外界と車とを唯一、物理的に繋げているとっても重要な部品、「タイヤ」の話をしてみましょう。
いきなりですが、始めにちょっと出題です。
「 なぜタイヤを太くするとグリップが上がるのでしょうか?」
この問題で重要な事は、「常識を疑ってみること」ですかね。
ちょっと考えてみてください。
ちなみに、タイヤの剛性変化や温度変化、トレッドのヨレなどは考えないとします。
まず、この質問の意味が分からない人は、ちょっと理論を勉強した方がいいかもしれないですね。
答えに悩んでしまった人は、物理が分かっていますね。きっと普段から考えているのでしょう。
答えがすぐに分かった人は、自分で考えたのだったら優秀です。
実はこれは、昔ある掲示板に質問が載っていたのですが、皆悩んで、結局誰も答えられなかった物です。
私も、確信を持つまでは、少し考えました。
もしかしたら 中途半端に物理の知識がある人の方が、ハマる問題かもしれませんね。
「タイヤは太けりゃ喰うだろー?」みたいな人が、結果的に当たっていますが、あくまでテーマは「常識を疑ってみること」です。
そのためには、いい問題だと思います。
それでは解説に入りましょうか。
さて、「太けりゃ喰うだろー?」と言うのは、正確に言うと「接地面積が増えるから摩擦力が上がる」と言うことでしょう。
一見最もらしいですが、ここで、自動車に必要な物理学に書いた摩擦の物理の法則を思い出してください。
摩擦力は、
F=μmg [N]
でしたね。
mは荷重、gは重力です。車重と重力は変えることはできないので、Fが大きくなるということは、タイヤを太くしたことで接地面積が変わり、μが大きくなっているはずですね。
しかし、物理学的にはμは物質特有の定数で変わりません。
少し分かりやすく説明してみましょう。
タイヤの接地面積は、葉書1枚分と言われていますが、タイヤを太くしたり、外形を大きくすれば当然接地面積も大きくなります。例えばバスのタイヤの接地面は、葉書1枚ではないですよね?
(と言うか、昨今の18インチや20インチの太いタイヤを履いたスポーツカーばかり販売される時代に、葉書1枚っていつの時代の話をしているのかと思います(笑)。)
さて、それでは葉書1枚分だったタイヤを太くして、仮に葉書2枚分の接地面積になったとしましょう。
これで摩擦力(グリップ)が上がるでしょうか??
これは高校物理の解答では、上がりません。
例えば、車重が2000Kgの車だったとしましょう。4輪にかかる荷重がすべて同じ車だとすると、1輪にかかる荷重は500Kgですね。
つまり、葉書1枚の面積に500Kgです。
摩擦係数μは、仮にタイヤの平均の0.9としてみましょうか。
すると、ノーマルタイヤの摩擦力は、
F=μmg [N] より、
F=0.9×500×9.8 [N]
ですね。
さて次に、太いタイヤにすると、接地面は倍の葉書2枚の面積になるので荷重は1000Kgになる、、、訳ありませんね。
車重は変わらないので。この場合は、葉書1枚当たりに、それぞれ250Kgずつ荷重が載っていることになりますね。
タイヤの材質はもちろん同じなので、μは同じです。
よって、
F=0.9×250×9.8+0.9×250×9.8 = 0.9×(250+250)×9.8 [N]
=0.9×500×9.8 [N]
ですね。
さて困りました。どちらも同じ摩擦力です。
つまり、接地面が増えた分、単位面積当たりの荷重が減ってしまうわけです。
よって、摩擦力はプラスマイナスゼロで、グリップは変わらないはずです。
質問の意味が分からなかった人は、ここまではいいでしょうか?
これが、高校物理での正解です。
イメージがわかない人は、消しゴムを思い浮かべてください。
消しゴムを寝かせて引っ張っても、立たせて引っ張っても、摩擦力は変わらないですよね?
寝かせた方が、接地面積は大きいのにです。
しかしながら、現実の世界では、タイヤを太くすると摩擦力は確かに上がります。
さてさて、何故でしょう?
それではまず始めに、
「なぜタイヤを太くするとグリップが上がるのでしょうか?」
と言う出題について、正確な答えを書いてみます。
それは、
「荷重と摩擦力(グリップ)の非線形性のため、μの線形領域がタイヤの太さによって変わるから。」
です。ちょっと難しいですねぇ(笑)。
簡単に言うと、現実の世界ではタイヤに1.1倍の荷重をかけると、グリップもキチンと1.1倍になりますが、1.5倍だと1.4倍、2倍だと1.6倍にしかグリップは上がらない、と言った状態になるのです。
だんだん荷重に対してリニア(直線的)にグリップが上がらなくなってくるんです。
そこでタイヤを太くして接地面を増やしてやると、例えば2倍の荷重で1.6倍だったのが、1.8倍のグリップになるといった感じです。
つまり、タイヤが太いほど荷重に対してリニアな領域が増える訳です。(勿論タイヤの銘柄は同じとします)
ちょっと荷重と摩擦力の関係の図を書いてみましょうか。
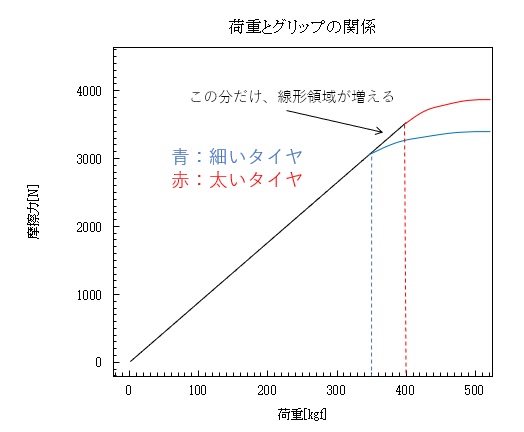
図のように、現実の世界ではμは変化し、タイヤを太くするほど図に示した線形領域が広がるわけです。
何だか、裏の裏は表みたいな問題ですね。中途半端に知識がある人の方が間違えるかもしれませんね。
「太けりゃグリップしそうだろう!」って人の方が、結果オーライな問題でした(笑)。
さて、ここで終わっては意味がないですね。
ここでの重要な問題は、「それではタイヤは太ければ太いほどいいのか?」
という話です。
確かに太い程、荷重に対するグリップのキャパが大きくなることは間違いありません。
しかしながら今回の例だと、どうあがいても1輪に2000Kg以上の荷重が掛かることは有りませんね。車重が2000Kgなんですから。もっと言えば、いくら大きな荷重移動があっても、現実には1000Kg以上掛かることも恐らくないでしょう。
つまり、最大荷重時に摩擦力が線形領域内に入っていれば、それ以上太くしても「全く無意味」だということです。
図で言うと、細いタイヤは350Kgの荷重をかけた辺りから、グリップがリニアに上がってくれなくなります。
太いタイヤでは、400Kgの荷重をかけた辺りまでは、グリップがリニアに上がってくれます。
つまり、400Kgの荷重をかけた時には、太いタイヤの方が摩擦力(グリップ)が大きくなりますが、350Kg以下の場合はどちらも変わらないことになります。
つまり最大荷重に対して、図の線形に近いグリップを発揮してさえくれれば、それ以上太くしてもメリットはなく、むしろ転がり抵抗や空気抵抗の増加や重量増、ハンドルブレーキなどのロスの方が増えてしまうでしょう。
簡単に言うと、エンジンの貴重なパワーが喰われるわけです。
だから、おいしい領域をキープできる、ギリギリの細いタイヤが一番速く走れるはずですね。
そして最適なタイヤのサイズはどうやって決まるのかと言うと、基本的に車重で決まります。 (ダウンフォースが無い場合)
図のタイヤで言うと、一つのタイヤに350Kg以上の荷重が掛かる事が無い車の場合には、それ以上太くするメリットは無いことになります。
まあ実際に、スポーツモデルでも軽自動車のタイヤは細いし、R35GT-Rのタイヤは太いですよね。
これは、基本的には車重が違うからです。
この基本理論により、自分の車に最適なタイヤの太さが計算できると思います。
ちなみに、それを正確に計算しているのが「メーカー純正」タイヤです。よって、これを基準とするのがよいでしょう。
最適な太さのタイヤに、最適な荷重をかけてやる事で、最大限にタイヤの性能を引き出せるわけですね。
実際に、初めて筑波サーキットで1分を切ったS2000は、最後にフロントタイヤの大幅なサイズダウン(結局純正サイズに戻した)を行って一気に1分切りを達成したそうです。
いかに無駄にタイヤを太くせずに、正しい荷重移動でグリップを上げることが大切かがわかりますね。
正しい荷重をかけて曲げたり止まったり、トラクションを掛けれるなってから、次にダウンフォースを増やしたために、それでも限界を感じてから、初めてタイヤのサイズアップを考えるのが正しいステップでしょう。
しかしながら、タイヤのグリップの限界を上げるには、タイヤを太くする以外の別解が有ります。
つまり、タイヤは一切変更しないという解です。
それでは、ちょっと考えてみてください(笑)。
続く…