ブレーキング時のピッチングと荷重移動について
さて、サスペンションとブレーキ性能の関係はもう4年近く前に書いた記事で、書いた時の記憶が若干曖昧なのですが、今までに何度か(トータル6通くらいかな?)意見を頂いたのですが、最近同様の内容が非常に多いので、ちょっと腰を上げて加筆修正しておきます。
確かこれはロールと荷重移動の項を書く前に加筆修正しようとも考えたんですが、逆にロールと荷重移動の項を読めば、ブレーキングはそれを前後方向に置き換えるだけなので、容易に分かると思ってずっと放っておいたものです。
まあ、最近なんでもかんでも答えを書くことに疑問を持っているんですが、一応サスペンションとブレーキ性能の関係の項は、赤文字の部分だけ加筆しておきました。
上記の項では ブレーキング時の荷重移動において、重力の力だけしか言及されていませんでしたが、当然ロールと荷重移動の項の話の横Gと同じように、減速Gが重心をピッチング軸周りに回転させる力、つまりトルクとして掛かりますね。
さてー、それはそれとして時々頂いたり見たりする説明として、車のロール運動やピッチング運動を、タイヤもサスペンションも無い「床に置いた硬い箱」などを例として説明する話があります。
私もサスペンションとブレーキ性能の関係に、車体が完全な剛体(バネもなくボディも変形しない硬い物体)だとしたら、「ピッチングによる荷重移動は起きない」と書いていますが、まあ違う意見の人もいると思います。
例えばブレーキング時で考えるとしたら、車体が完全な剛体だとしても、モーメントによって車体の前輪に押し付ける力が掛かる、つまり荷重が掛かる、という考え方をする人がいるということですかね。
今回はこの話について、ちょっと書いてみます。
この皆さんが言う「モーメント」というのは、恐らく物理で言うところの、回転における「力のモーメント」(=トルク)の事を言っているのだと思います。 ピッチング運動を起こす力もこれということですね。
実際の車においては今までにロールと荷重移動の話などに書いた通り、重心にかかるトルクがロールやピッチングを起こして、タイヤを押し付ける力になりますね。
ま、これは皆さん同じ意見でしょう。
ただ図1の右のように、箱のような完全な剛体ではどうなるでしょう?
例えばこれを車にすると、サスペンションが付いていなく、ボディも一切シナッたり曲がったりせず、ブッシュやタイヤも一切潰れたりヨレたりしない、完全な硬い車だとしましょうか。(元は箱を置いただけの例なので、タイヤの経はとても小さいとします)
この車にも力のモーメント(=トルク)が働いて、そのモーメントがブレーキング時に前輪の荷重を増やすのでしょうか??
ふむ。まずこの車に力のモーメント(以下モーメント)自体は掛かりますね??
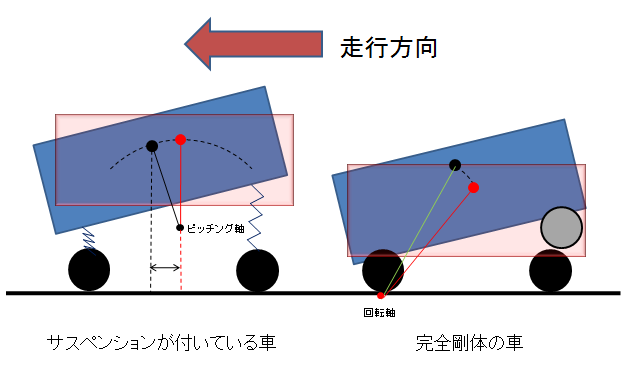
図1 完全剛体の例
その前にモーメントの定義はいいですね? モーメントとは、自動車に必要な物理学、あるいはWikipediaを見てもらってもいいですが、ある軸を中心とし、そこから力を与える点への位置ベクトルと、力点に掛かる力のベクトルの外積です。
簡単に言うと、回転の中心軸から力を与える点の距離に、円の接線方向の力を掛けたものです。
接線方向の力ですから、当然半径方向、つまり「回転の軸を動かす方向の成分」は含まないものです。
これが物理的な定義です。
それを踏まえて図1の完全剛体の車の、ブレーキング時の回転軸はどこでしょうか?
サスペンションも付いていないので、重心が回転運動をするとしたら前輪の接地面を中心とした回転運動となりますね?(完全に引っ繰り返ったりはしないとします)
つまりこのケースでは、荷重を与えられる点(前輪の接地面)自体が、回転軸となってしまいます。
この回転運動を、果たしてピッチング運動と呼ぶべきかどうかは置いておいて、もしこれをピッチングと呼ぶならば、加速時と減速時でピッチング軸が車の端から端まで移動することになりますね?
同じくローリングなら旋回方向によって、右端から左端までロール軸が移動します。
まあ、一般にはこれをピッチングやローリング運動とは呼ばないようです。
私はこの運動のことを、ピッチングやローリング運動と区別して「引っ繰り返り運動」と呼んでいます。
そして次に、この「回転軸を押し付けようとする力」を、果たしてモーメントによる力と呼ぶべきか?、という話です。
上記の通り、物理学的にはモーメントとは、力の回転させる方向の成分と軸までの距離を掛けたもののことを言い、軸自体を動かそうとする力は、そう呼びません。
例えば、図2の様にプロペラを指で押して回すとしましょうか。プロペラに対して完全に垂直に押せば回転軸を動かす力はゼロですが、図の様にちょっとでも斜めに押すとその力はプロペラを回す力と、回転軸を動かそうとする力の両方が掛かりますね?
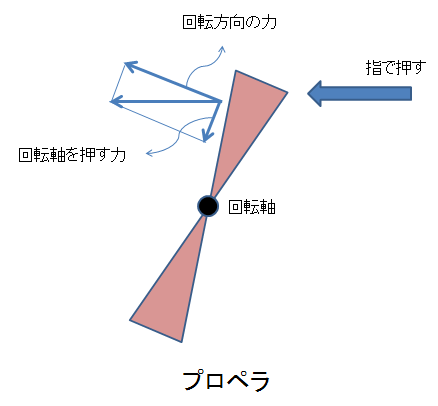
図2 斜めにプロペラを押す例
このプロペラの回転軸を押して動かそうとする力は、モーメントでしょうか?? まあ、普通は違うと考えるでしょう。(少なくとも、物理学ではそう呼びません)
同じく完全剛体の車の回転軸(前輪接地面)自体を押す力は、厳密には「モーメント(トルク)」と呼ぶのは正確ではないかな、と思います。 トルクレンチで、ボルトを前後方向に動かす力をトルクと呼ばないのと同じですかね。
(ま、そこまで物理的な厳密性にこだわらなければ、広義でこれもモーメントによるものとしても、そのほうが理解しやすければ特に問題はないのかもしれませんが・・・、でも個人的には勧めませんかね。)
また他には、「この場合には前輪の接地面と重心とを結んだ線の中間辺りに見えない回転軸が存在し、その仮想的な軸の周りにモーメントが働いている」、という考え方もあるようです。
ただそうすると、実際に回転運動をする回転軸と、もうひとつの実際に回転運動は起きないが、仮想的な回転軸という2つの軸について考えなければなりません。
しかも厄介なことに、その2つ目の回転軸自体が回転運動をします。
これをプロペラの例にすると、プロペラの回転軸を押す力は、指でプロペラを押す点と、固定された回転軸との中間辺りに仮想的な回転軸があり、その周りに働くモーメントによる力である、、、。
とするよりも、「回転軸を押す力は、指でプロペラを押す力の鉛直方向の成分である」としたほうがシンプルですよね?
まあこの様な2つ目の仮想回転軸を作るようなモデルは複雑なので、純粋に前輪の接地面を押す力は、「重心の慣性による力の縦方向の成分によるもの」と考えたほうがシンプルで良いでしょう。
つまりこの完全剛体のケースでは、「ピッチングモーメントによる荷重移動はしない」と私はしています。
ま、「どうしても仮想軸を作ってモーメントとして考えたほうが理解しやすい」、という人はそれでも特に問題はないでしょう。
どっちにしろ結果は同じですからねっ。 ブレーキング時には前荷重となりますし、その荷重は車重を超えることはありません。
(ただこのように何でも力のモーメントで考えると、その回転軸自体を動かそうとする力を考慮するのを忘れるケースがあるから注意が必要です。
例えばサスペンションが付いている普通の車でも、車が独立した系(外部から力を与えられない)とすると、Gによってピッチング軸自体を動かす力が掛かりり、Gが大きくなると動くことがあります。
仮に独立した系ではなく外部から、例えば壁から頑丈なワイヤーでピッチング軸を固定すればGによるピッチングモーメントは理論上は無限にかかるのかも知れませんが、当然現実にはそんな事はないので、ピッチングモーメントは無限には掛かりません。
よってもちろん、荷重も無限には掛かりませんね(車重を超えない)。)
まとめると、
1、完全剛体の車では、重心の回転軸が前輪接地面や後輪接地面となり大きく移動するため、この回転運動を一般にはピッチングとは呼ばない。
2、仮にそれをピッチングと呼んだとしても、ブレーキング時の荷重移動はピッチングモーメントによるものではない。
といった感じです。
これらの事から、「完全剛体の箱」を車のモデルとして考える例は、あまり良くない例だと思います。
また上記より、「完全剛体にすると、ローリングやピッチング運動と呼ぶべきものは存在しない」、というのが私の考え方です。
もちろん、現実の世界にはこのような完全剛体の車は存在しないため、必ずピッチング軸は前輪と後輪の間に存在するはずです。
その場合には、先述のように軸の周りにモーメント(トルク)が働き、それも前輪の荷重を増やす力になります。
ちなみに仮に上記の完全剛体のタイヤが潰れただけでも、回転軸は前輪の接地面にはなりませんね?
ここでいう回転運動とは円運動ですから、円の定義自体がある点から平面上の等距離にある点の集合なので、重心と前輪の接地面との距離がタイヤが潰れて変わった瞬間に、そこは回転軸ではなくなります。
(タイヤが潰れきるまでの間は、恐らくホイールベース内のどこかにピッチング軸が有るでしょう。)
まあ今回書いたことはちょっと難しかったかも知れませんが、ちょっと私の考え方を書いておきました。
出来るだけ分かりやすさを優先して書いたつもりですが、 興味がある人以外はここは特に理解しなくてもオッケーの部分です。
これからもこのHPでは今までのコンセプト通り、出来るだけ分かりやすさを優先して高校物理からはみ出ない、シンプルなモデルで考えて行く予定です。