コーナリングの最適解 その1
さて、今回はアウト・イン・アウトとスローイン・ファストアウトの話にプラスして、最適解へのアプローチ(序論)に書いた内容を取り入れて、あるコーナーを一番速く曲がる走り方、「最適解」について考えてみます。
サスペンションを物理するにあたり に、
「コーナーには最適なラインが有って、常にギリギリにRを大きくする「アウト・イン・アウト」で走るラインが一番速いとは限りません。
どのラインが最適かは、車などによって変わり、ケースバイケースです。
スピードの出ない車であまり大きなRにすると、「単に遠回りしているだけ」になりますよね?
この場合はスピードのロスよりも、遠回りする事による距離のロスの方が大きくなる、それが入れ替わるポイントがどこかに有る訳です。
何度も言いますが、全てには「最適値が有る」のです。 それを常に念頭に入れておいてください。」
と書きましたが、今回はその「最適解」とは何か?を、具体的に考えてみようというものです。
昔から「アウト・イン・アウトラインが速い」と漠然と言われていますが、実際に他の小さく曲がるラインと比べてどれくらい速いのか、可能な限り大きく曲がったほうが速いのか、それともあるレベル以上に大きく曲がると逆に遅いのか、ちゅうか、そもそも遠回りしているのに本当に速いのか?といったものを数学的に証明したものって、見たことがありませんよね??
距離損とスピード損
に書いた、アウト・イン・アウトラインの話も、「偶然に区間タイムが同じだったら」、という仮定の下での話でしたね。 今回は実際に区間タイムもどうなるのか調べてみましょう。
それではここで一つのモデルを作って、それを経験則ではなく物理的、定量的に調べてみようと思います。
今回はモデルとして、図1の様な180度曲がったコーナーを考えてみましょう。
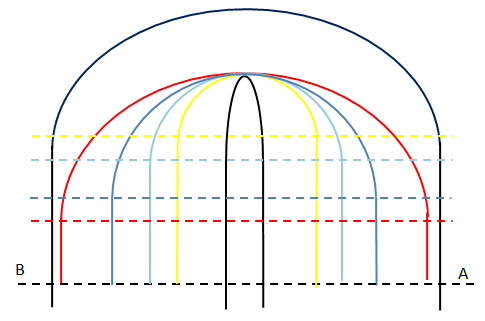
図1
Rの異なるコーナーのライン。
Aが進入位置で、Bが出口です。
色んなラインを試せるように、このコーナーは道幅が広く、ラインの曲率(R)の選択幅が図1の様に広いとします。
さて、ここで一番小さく曲がるラインが黄色ですね。
逆に一番大きなR、つまり大きく曲がるアウト・イン・アウトラインが赤のラインですね。
その間にも、その中間のライン(図1の青と水色など)が無限にあることになります。
ここで実際に計算するに当たり、このモデルで幾つかの仮定をします。
まず、コーナーはどのRを通っても、180度の円弧を描くラインとします。
図1のA側の破線の位置が曲がり始める所で、B側の破線が曲がり終わる所です。
つまり、大きなRのラインほど早く(手前から)曲がり始め、小さなRのラインほど奥で曲がり始めるということですね。
これはいいですね?? 小さなRで手前から曲がり始めると、当然コーナーのイン側にぶつかりますね?
よって小さなRで曲がるということは、必然的に奥まで突っ込んだ運転となります。
例えば黄色のラインならば、黄色の破線の位置までは直線として走り、破線の位置で曲がり始めるということです。
つまり突っ込み重視の運転は、結果的に小さなRを描く運転をしていることになりますね。
これ、意識してるかな??
次に大きなRの場合ですが、180度も円弧を描く必要はないと考える人も居るかな??
ただ、大きなRの円弧で黄色いラインのような位置まで突っ込むと、直線から円弧に変わる場所で鋭い「カド」が出来ますよね?
そのようなカドは遠心力が極端に大きくなって車は曲がることが出来ないため、どんなに大きなRでも180度曲がるラインとします。
これは逆に言えば、大きなRで曲がろうとすると、必然的に奥まで突っ込んだ運転とはならないことが分かると思います。
アウト・イン・アウトラインも、もちろんそうです。
次に、Aの進入位置では、どのラインでも同じ速度とします。
またブレーキングの終了位置は、それぞれのラインに対応する色の破線の位置とします。 これはつまり、Rの始まる位置です。
ブレーキングは、最適解へのアプローチ(序論) に書いた最大の減速Gである、μ[G]
を発生するとします。
また、Aの侵入位置からブレーキを踏み始めるまでの間は、速度は変化しないとします。
これは簡単に言えば、Aからブレーキング開始ポイントまでは、どのラインでも加速せずに等速であるということですね。
Aからブレーキング開始ポイントまで加速しないというのは現実のモデルと少し異なるかと思いますが、加速するとすると計算が複雑となるため、今回はこの様に仮定します。
またコーナー終了地点(破線)からBの位置までの直線区間の加速は、一定の加速Gを保つとします。
これも実際の車は、速度が上がるほど加速Gは落ちてきますが、計算を簡単にするために一定の加速Gとします。
これは平均の加速Gと捉えてもらっても良いでしょう。
そして最後に、コーナリング中の速度はRの始まりから終わりまで(破線から破線の間)常に、最適解へのアプローチ(序論) に書いた通りの、遠心力でギリギリ滑らない一定の速度を保つとします。
これを大回りしているのに小回りしている時と同じ速度にするなど、限界のはるか手前で走っていたら当然遅いでしょうから、この仮定は自然でしょう。
なお、実際のコーナリングでは一般に旋回中にも加減速をしますが、これも加減速を伴うと非常に計算が複雑になるため、ここでは旋回速度は一定とします。
このモデルの仮定は、以上です。
物理学というのは、「複雑すぎて難しいから解けない」とするよりも、多少の近似をしたり単純化したモデルを作ってでも、なんらかの定量的な答えを出そうとする学問です。
そのため、質量だけが有って大きさのない「質点」とか、摩擦のない「滑らかな床」といった話が高校物理でも良く出てきたと思います。
余談ですが、高校物理の初期の方で習う「振り子」の運動も、運動方程式を解く際にsinθ=θ といった結構大胆な近似をしており、実際には振り子の運動に解析解(一般解)は存在しません。
よってもちろん正確には単振動にもならなければ、周期も振り幅が変われば一定ではありません。
ただ現在では、コンピューターの進歩によって解析解の存在しない運動方程式でも、「数値解法」で非常に誤差の少ない解の計算が出来る事も覚えておくと良いと思います。
今回のモデルも、上記の様なある程度単純化したモデルであることを覚えておいて下さい。
さて、それでは以上のモデルで、それぞれのラインごとのA地点からB地点までの、コーナーの区間タイムを実際に計算してみましょう。
このモデルでは、A点を過ぎてからブレーキを踏むまでの時間、ブレーキング時の減速中の時間、旋回区間の時間、旋回区間が終了してからB点までの直線区間の時間、の4つに分けて計算する必要があるでしょう。
まず始めに、旋回区間のタイムを計算してみましょう。
これは、最適解へのアプローチ(序論) を読めば簡単ですね?
旋回半径をr とすると、遠心力の式は、F =
mv2/r でしたね?
これがタイヤの摩擦力と等しくなる速度が、タイヤが滑らないギリギリの速度となりましたね。
よって車重をm、タイヤの摩擦係数をμ、重力加速度をg、とすると旋回速度v は、
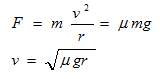 ・・・式1
・・・式1
となりましたね。
速度がわかったので、距離がわかれば時間がわかりますね?
今回は180度の円弧を回るので旋回区間の距離は円周の半分ですね?
つまり距離は、2πr/2 = πr
となります。
よって、旋回区間のタイムは走る距離を速度で割ってやって、
![]() ・・・式2
・・・式2
ですね。
これで旋回区間のタイムが分かりました。
それでは次に、ブレーキングしている時間を計算してみましょう。
A点での速度をv0、ブレーキングの制動Gをa とすると、式1の旋回できる速度v まで減速するまでの時間は、速度差を加速度で割ってやれば良いですね?
よって、![]() ・・・式3
・・・式3
で計算できますね。
これがブレーキングをしている時間です。
それでは次に、A点を過ぎてから、ブレーキングを開始するまでの時間を計算してみましょう。
これはちょっと面倒ですかね。
図1より、A点を過ぎてからブレーキングを開始するまでの距離と、ブレーキング中に走る距離を足したものは、選択するラインのrによって変わりますね?
具体的には、A点から破線までの距離になります。
その距離をΔRとしてA点の位置をRとすると、図1よりΔRはR-r となりますね?
つまり、r が大きくなる程ΔR が小さくなるのが図1より分かると思います。
この距離ΔRが、ブレーキングを開始するまでに走る距離とブレーキング中に走る距離を足したものになるので、ブレーキングを開始するまでの時間をts、t を式3で計算したブレーキングをしている時間とすると、
![]() ・・・式4
・・・式4
となりますね?
この式4のt に式3で計算したt を代入して、ts について解いてみると、
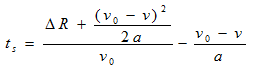 ・・・式5
・・・式5
となります。(皆さんも是非検算してみて下さいね)
これで、コーナーの侵入地点から旋回区間終了地点(破線)までの時間が出ました。
後は旋回区間終了地点(破線)から、B点までの直線の時間を求めればいいですね。
これは簡単ですね。
旋回速度を式1のv、加速度をa、B点までの時間をt とすると、
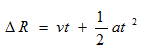 ・・・式6
・・・式6
ですね。
これをt について解いてやればいいですね。
ちょっと解きやすいように両辺を1/2aで割ってやると、
![]() ・・・式7
・・・式7
ですかね。
さて、解けるかな??(笑)
なんか中学時代に習ったような記憶を思い出して…
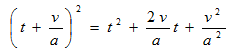 ・・・式8
・・・式8
を利用してやると、これから余分な最後のv2/a2を引いてやれば式7の右辺になりますね。
これを利用して、式7をt について解いてみると、
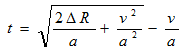 ・・・式9
・・・式9
となりますね。
ふー、お付き合いお疲れ様でした(笑)。私も疲れました(笑)。
これですべての区間の時間が求まりました。
旋回区間の式2、ブレーキングを踏んでいる時間の式3、A点からブレーキング開始までの区間の式5、加速区間の式9を全て足してやれば、このコーナーのA点からB点までの区間タイムが出ますね。
後はこれらを計算して、r の変化ごとにコーナーの区間タイムのグラフを書いてみれば、ラインの最適解が分かりますね。
それでは休憩を兼ねて、続きは次回にします。
その気になればExcelでもグラフは書けると思うので、皆さんも挑戦してみてはいかがでしょうか。