コーナリングの最適解 その3
さて、前回の続きです。
それでは旋回区間のタイムが分かったとして、次にコーナーの出口B点の速度を計算してみましょう。
いわゆる、コーナーの「脱出速度」というものですね。
コーナリング終了地点からB点までの時間はコーナリングの最適解 その1の式9で求めた通り、
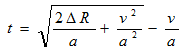 …式1
…式1
ですね。
自動車に必要な物理学
より、加速度に時間を掛けたものが速度でしたね?
加速度をaとすると、
![]() …式2
…式2
が旋回区間の終了場所からB点までの速度の増加になりますね。
旋回区間の速度をvとすると、それに上記の増加分を足したものがB点の速度となりますね。
よってB点の速度は、
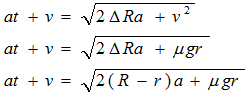 …式3
…式3
となります。ここでRはA点とB点のクリップからの距離(定数)、rはコーナーのRです。
ここでルートの中にちょっと注目してみると、![]()
この式が、ある加速度の時に面白いことになります。
加速度がタイヤによる限界加速度のちょうど半分の時にどうなるかを計算してみると、
![]()
といった具合にrが消えて定数となります。
よってこの時のB点の速度は、
![]() …式4
…式4
となり、なんとコーナーのR(ライン)によって全く変化しないことになります。
余談ですが、たまたま始めに1/2μg [m/s2]という加速度で計算したら、Rを変えても全く速度が変わらなかったため、計算ソフトの不具合かと思ってしばらく悩みました(笑)。
それでは上記の式3を使って、Rの大きさとB点の速度の関係を計算してみましょう。
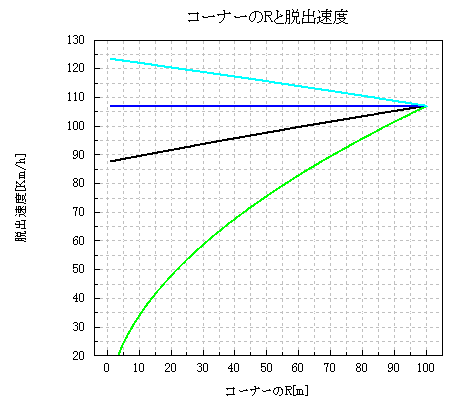
グラフ1 コーナーのRと脱出速度の関係
緑色の線はコーナリング(旋回区間の)速度です。
黒い線は0.3[G]の時、水色の線は0.6[G]の時、そして青い線が上記の、1/2μg
[m/s2]=0.45[G]の時です。
全て一直線になっていますね。(正確には青線以外は直線ではないが)
この結果も非常に興味深いですね。
前回書いた区間タイムも、加速力が0.45[G]から一番速いラインが極大値を持つかどうかが変化しましたが、B点の速度のグラフの傾きもちょうど0.45[G]から変化しています。(これは上記の式4の通り、数学的に証明しました)
つまり加速力が0.45[G]よりも小さければ、大きなRになるほどB点の速度は高くなります。
そして上記の式4から、0.45[G]の時にはRによってB点の速度は全く変化しません。
そして加速力が0.45[G]よりもよりも大きくなると、Rが小さいほどB点の速度は高くなります。
これは個人的に、とても興味深い結果だと思いました。
つまり車の加速度がタイヤの摩擦係数μ の半分よりも小さければ、区間タイムとB点の脱出速度が共に、Rを大きくすればする程速いことになります。
よって区間タイムだけでなくコースのタイムも、
「旋回中に最大限の横Gを維持できる中で、最大の大きなRを描くラインが一番速くなる」
という結論となりますね。
そして加速度がちょうどμ/2[G](今回は0.45[G])の時には、区間タイムはRが大きい程速くなりますが、B点の脱出速度はRによって、つまりラインによって全く変わりません。
よってB点の速度が変わらないのならば、区間タイムが一番速いラインを選べばコースのタイムも一番速くなりますね。
よってこの時も、出来る限り大きなRをとった方が速いことになります。
余談ですが、1200Kgの200馬力の車で、100Km/hからの加速がちょうど0.45[G]となります。
この数値って、、、ほぼBRZ(TOYOTA 86)の数値ですね。
そして注意すべき所が、加速度がμ/2[G]よりも大きい時です。
この時には必ずしも最も速いラインは、このコーナーのラインだけでは決められないことになりますね。
例えば加速度が、上記のグラフ1の0.6[G] の時に区間タイムの方はどうなるかを見てみると、
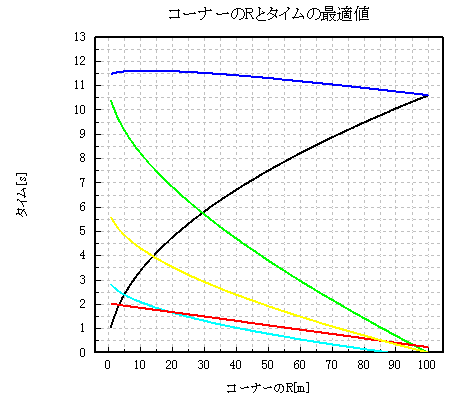
グラフ2 コーナーのRと区間タイムの関係
となります。
15R辺りに極大値はありますが、概ねRを大きくする程に一直線に区間タイムは速くなっていますね。
ところがグラフ1より、Rを大きくすればする程B点の速度は遅くなります。
つまりここで、区間タイムを犠牲にしてB点での脱出速度を優先するか、或いはB点の速度を犠牲にして区間タイムを優先するか、といった選択をしなければなりません。
或いはその中間のRをとって、区間タイムと脱出速度の両方を、それなりに速くなるようにするのも一つの答えでしょう。
さて、それでは
この0.6[G]の加速度の時に選ぶべきラインは何で決まるでしょうか??
それが前回コーナリングの最適解 その2に書いた、「このコーナー区間がコースの中でどのようなポジションにあるか」ということで決まります。
簡単に言えば、B点の先の直線区間(でなくてもアクセルを全開に出来る区間)がどれだけの長さがあるかによって、どのラインを選ぶのが一番「コースのタイム」が速くなるかが決まるでしょう。
当然B点の先ですぐにブレーキを踏まなければならないコースならば区間タイムを優先するべきでしょうし、B点の先の直線がとても長ければB点の脱出速度を優先するべきでしょう。
そして
もちろん、その最適値は車の加速力によっても変化します。
今回は0.6[G]としましたが、例えば加速度が、摩擦係数μが0.9のタイヤを履いた車の限界の加速力である0.9[G]だと、より一層小回りの優位性が出てくることも分かりますね。
コーナリングの最適解 その2のグラフ4より、区間タイムも小回りした時が最も速くなる上に、脱出速度も小回りが最も速くなるからです。
ただ加速力が0.9[G]の車というのは、相当なハイパワーで高トラクションの車でないと無理でしょう。
(これは0-100Km/h加速だと、3.1秒で走れる車の平均加速度です。)
ちなみに100Km/hから0.9[G]の加速をしようと思ったら、約400馬力が必要です。150Km/hからなら約600馬力がです。
逆に低速ならば、少ないパワーでも大きな加速力を出せます。
この辺の話について詳しくは、エンジンの話を見て下さいね。
よって今回のモデルよりコースを最も速く走るためには、旋回区間の終わりからB点までの平均加速度が0.45[G](μ/2[G])以下の時は迷わず前回の区間タイムが一番速くなるラインを選び、平均加速度が0.45[G]よりも大きい時には、加速度とB点から先の直線の長さによってラインを変える必要がある、といった感じでしょう。
これは平均加速度が0.45[G]よりも大きい車では、
区間タイムが遅くても脱出速度が速いと、先の直線で逆転することがあるからです。 (この加速度とは、B点までの平均の加速度であることに注意して下さい。)
それがどういった条件の時に逆転するかは、車の加速度とB点から先の直線の長さからぜひ計算してみて下さい。
どこかに最適値があるはずです。
計算は自動車に必要な物理学を読めば簡単でしょう。
必要なのは位置と速度と加速度の関係だけのなのでとても簡単ですが、一応書いておくと、
加速度がa、速度がvの車が、時間t経った時の速度は、
速度 = v + at
時間tで進む距離は
距離 = vt + 1/2at2
となります。
これだけで計算できるはずです。
また上記のような加速度が0.9[G]に近いような車では、区間タイムの極大値が右に移動し、Rが小さい所に区間タイムの最速値も来るので、Rが小さい程区間タイムと脱出速度共に速いことになりますね。
ただ小さく曲がるRには限界があると思うので、小さめにしたRがちょうど区間タイムの極大値にはまってしまっていないかは、注意が必要でしょう。
昔は一般にアウト・イン・アウトラインが一番速いとされていたようですが、ある時期から(10年ちょっと前くらいかな?)車によっては「V字型の様なラインの方が速い」と言われるようになって来たようです。
(V字ラインというのは、今回のモデルのRを出来る限り小さくしたものを、少しだけ変形したものと考えて良いでしょう。)
ちなみにそのV字ラインの方が速い車とは、多くの場合ハイパワーの4輪駆動車のようです。
つまりタイヤの性能が上がり、縦グリップ(μ)が大きいタイヤで4輪駆動でハイパワーのターボ車が、サーキットでタイムを競い始めた頃だと思います。
その様な強力な加速力を持った車では、従来通りのRを大きく取ったアウト・イン・アウトラインよりも、「直線的に入って小さく曲げてドンと直線的に立ち上がる」といったV字的なラインの方がタイムが出ることが、恐らく経験的に分かってきたのだと思います。
そしてそれは、今回の計算より理論的にも正しいことが証明できたと思います。
ちなみに今回のモデルでは簡略化のためにA点からブレーキング開始ポイントまでは加速しないとしましたが、実際には加速するはずです。
Rを小さくすれば、より加速区間は長くなるでしょう。
(ただ速度が上がれば当然手前からブレーキを踏まなければいけないので、立ち上がり加速ほどの影響はありません)
よって加速力の高い車であれば実際には、より一層小さなRのラインの優位性が出てくる(区間タイムが速くなる)ことも付け加えておきます。
また今回のモデルの簡略化による誤差は、パワーだけではなくA点での速度によっても変わります。
例えばA点の侵入速度が200Km/h等の高速だといくらハイパワー車でもそこから高い加速Gは望めないため、今回の等速モデルと比べて誤差は少ないですが、A点で低速ならば高い加速Gを出せるため、今回の簡略化による誤差が広がるはずです。
以上、今回の結果をとっても簡単に
まとめると、「ハイパワーな車で立ち上がった先の直線が長い低中速のコーナーでは、小さなRで曲げて直線区間を多く取った方がコースのタイムは速くなるが、高速コーナーやパワーがそれほどない車では、限界の横Gが出せる中で出来るだけRを大きくとった方が速い。」
といった感じですかね。
とりあえず今回のモデルの計算と考察は以上です。
いかがでしたでしょうか??
どこかの漫画にも、「コーナーを立ち上がった先の直線の長さによってコーナーのラインが変わる」といったようなことが書いてありましたが、その理屈は今回の話と同じでしょう。(加速Gが0.45[G]よりも大きい車なのでしょう)
久しぶりに、最後に一つ出題です。
F1などのレーシングカーは、ハイパワーで高トラクション(最大で1.5[G]の加速Gが出るらしい)なのにV字ラインでは走っていませんよね??
アウト・イン・アウトラインに近いラインだと思います。
これはなぜだか分かりますか??
答えは書きませんので、考えてみて下さい(笑)。
ヒントは「空力」です。(ほとんど答えですが)
それでは次回は、実践編を少しだけ書いてみようと思います。
続く…。