荷重は無限に掛かるのか?
さて、まず始めにちょっと荷重の話をしたいと思います。
私は 車の足廻りやコーナリングを考える事は、極論を言うと荷重のコントロールを考える事だと考えています。
そこで今回は、非常に重要なのに、意外と勘違いの多い「荷重」の話について書いてみます。
まず始めにとっても重要な事を。
例えば、車がコーナーを曲がっているとします。 その時に、外側のタイヤに掛かる荷重が増えるはずですが、もしもタイヤが滑らないとしたら、荷重はどこまで増えるでしょうか??
今回の話は、空力によるリフトやダウンフォースは無視します。
以前に、「車をロールさせる力はモーメントと言う重力とは違う力による物で、モーメントが増える限り、つまりタイヤが滑らないとすると、同じコーナーでスピードを上げれば理論的には無限に荷重 が掛かる」
という説明を読んだ事が有ります。
また、荷重移動を表す数式でも、無限に外輪の荷重が上がると取られる様な式を、何度か見た事が有ります。
確かに、車に横Gが掛かると、遠心力が車の重心をロール軸の回りに回転させて、外側のタイヤを路面に押し付けようとする力が働きます。
もしもタイヤがとてつもなくグリップが高くてどこまでも滑らなければ、この押し付けようとする力はスピードを上げて行けば無限に掛かる、様な気もしますかねぇ。
車のロールと荷重移動の話は、後に詳しく書くのでここでは数式は省略しますが、この理論は一理ある様な気もしますかね?
ここで言うモーメントと言うのは、力のモーメントの事で、別の呼び方をすれば「トルク」ですね。
トルクは、理論上は上限は有りません。 無限に掛けられそうな気もします。
まずは、これを書いた人の気持ちを理解してくださいね。 それが先です。
しかし答えから言うと、4輪が沈むブレーキは可能なのか?項に書いた様に、平地を走っていて、空力を無視する限り、車には車重以上の荷重をかけることなど出来ません。
ところが、これを数式を使って厳密に証明しようとすると、意外と厄介です。
と言うか、車の動きの精密なモデルを作る、つまり数式を立てるのが大変なんですよね。
足廻りの形式の違いや、トレッド、重心、ロール軸などは、車によって違いますからねぇ。
まあ、ここでは後で数式を使って説明しますが、普通の人はそこまでやる必要はないでしょう。 時間がもったいないですから。
そんな時に重要となるのが、「物理的に物事が考えられるセンス」です。
いいですか?
「独立した系において、水平方向の力を垂直方向の力に変える事は不可能なのです。」
車の例で簡単に言うと、外部から力を与えられない限り、横方向の力である「遠心力」を、縦方向の力である「タイヤの荷重を上げる力」には、変えられないのです。
感覚的に何となくわかりませんか??
でわ仮に、上記に書いた様に、遠心力によって無限に荷重をかける事が可能だとしましょうか。
もしそれが可能ならば私は、以下の様な機械の特許を出願します(笑)。
それは、以下の図1の様に、まず円盤の上にミニチュアの車を載せます。
そしてタイヤと円盤の間は接着剤で固定して、絶対に滑らないようにします。
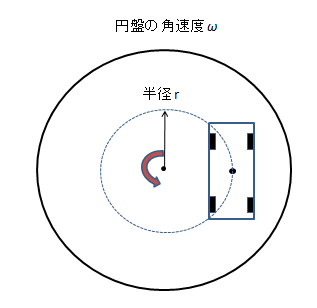
図1 車をミニチュア化したモデル(上から見た図)
次に、円盤を電気モーターでグルグルと高回転で回せるようにします。
つまり、ミニチュアの車がコーナーを曲がっている時と、同じ状態を作る訳です。
ミニチュアの車には、遠心力が掛かり、ロールして外のタイヤに荷重が掛かりますね。
そしてこの機械を円盤ごと、車に搭載します。
すると素晴らしい事が起きます。
何と、空力を使わなくてもモーターを回してやるとダウンフォースが掛かるのです!!
ミニチュアの車の荷重が、円盤の回転数と共に上がっていく訳ですから。
それもGTウィングなどの空力パーツと違って、モーターの回転数を上げる限り低速コーナーでも無限にダウンフォースを掛ける事が出来るのです。
ダウンフォースがいらない直線では、モーターを止めてやれば、ダウンフォースが掛からなくなり、転がり抵抗が減ってストレートも伸びますねぇ。
何とも最適な、ダウンフォース発生システムです。
もっと言えば、水平方向の力を垂直方向の力に変えられるのなら、遠心力を使って空を飛ぶ機械なんて物も出る事になります。ダウンフォースとは、力の向きを上下逆にするだけですから。 これは正に、プロペラの無いヘリコプターですね。
しかし、もちろん、こんな物は出来る訳は有りません。
感覚的にわかると思います。
これがすぐにわかるのが、「物理的なセンス」ってやつです。
しかし中にはこんな疑問を持つ人もいるかと思います。
「もしも、お茶碗の中に、パチンコ玉を入れて、茶碗の壁に沿って、どんどん高回転でパチンコ玉を転がしてやれば、遠心力でどんどんパチンコ玉が茶碗の壁を登って行って、上に飛び出すじゃないかー
」と。
しかしこれは、実は独立した系の中で起こって上に登る訳ではありません。
お茶碗の壁が斜めなので、茶碗を固定すると、壁が遠心力を上に変換しているのです。
実際に独立した系にするために、お茶碗を固定せずに宙に浮かせると、パチンコ玉が上に登ろうとする力の反作用でお茶碗が下に押されます。
つまり、パチンコ玉が上に行く代わりにお茶碗は下に行き、上下方向の力の帳尻は±0で、やはり合うのです。
この場合も、
遠心力によって縦方向の力の合計を増やす事は、やはり出来ないのです。
いいですね?
足廻りやコーナリングを考える上で、これから荷重の話はたくさん出てくると思います。
そして、平地を走る限り、この「4輪合わせた荷重はどんな時も変わらない」と言うのは、とても重要です。
「当たり前でしょー。」と思うかもしれませんが、ハマった時に思い出して下さいね。
「やはり実は変わるのでは?」と勘違いさせるような現象が、車でもバイクでも、結構起きる物なので。
例えば、バイクの例だとコーナリング中にサスペンションバネが縮んでいるから、コーナリング中には荷重が増えていると言っている人がいますが、バイクは傾けないと曲がらないため、その様になるだけです。
この場合、バネを縮めているのは縦方向の荷重ではなく、遠心力に対抗しようとするタイヤの摩擦ですね。
もしも傾けずに曲がれるならば、バネは縮みませんからね。
更にやっかいな例として、またまたバイクですが、後ろのブレーキだけ掛けると後ろのバネが縮むそうです。
しかしこれも、荷重が掛かってバネが縮んでいる訳ではありません。
ブレーキをかける事により、チェーンに掛かる逆方向力が、スイングアームの構造上バネを縮める力になるのです。
よって、バネが縮んでも後ろの荷重は増えている訳ではありません。
(厳密には、バイクが傾くと重心が移動して、少し後ろ荷重が増える事があるかもしれません。)
ね? 結構勘違いさせる現象が起きますよね??
最後にちょっと余談です。
私の経験からですが、物理の専門家でも、物理のセンスのいい人ほど、グダグダと数式を立てません。
計算もしません。 そんなことをしなくても、感覚的にわかるのです。
自動車に必要な物理学に書いた様に、エネルギーは保存する、運動量は保存する、角運動量も保存する、力を与えれば反作用を受けると言った、基本原理を理解すれば、数式などは具体的な数値が欲しい時以外には、殆ど必要ありません。
皆さんも是非、物理的なセンスを身に付けてみて下さい。 車はもちろん、多分、世界を見る目が変わるでしょう。
それでは次回からは、具体的な話に入って行きましょうか。