タイヤのグリップを超えたグリップ力を出す
さて、次にもう少し物理的にタイヤの縦方向のグリップ(摩擦力)と、横方向のグリップを考えてみましょう。
今回も1200Kgの車重の車を例とした、思考実験をしてみましょう。
また、今回もタイヤに掛かる荷重は全て同じとし、車体のロールやピッチングは存在しないことにします。
さて、下図1の様に車を横に置いて、滑車を通してオモリをぶら下げて、車が動き出す、つまりタイヤが滑りだすオモリの重さを計算してみましょう。
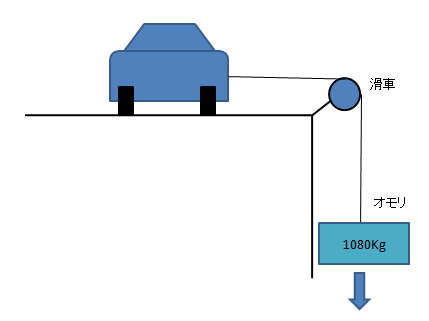
図1 横方向に引っ張る例
またまた出てきますが、タイヤの摩擦力は、
F = μmg
なので、摩擦円を物理すると同じく、μを路面とタイヤの平均の摩擦係数0.9とし、mは300Kg、gは9.8m/s2なので、
F = 0.9 × 300 × 9.8 = 2646[N]
となりましたね。
そして今回はこれが4輪有るので、
F = 2646 × 4 = 10584[N] = 1080[Kgf]
となります。
つまり、図の車を滑らせるには1080Kg以上のオモリを付ければいい事になりますね。
次に、下図2のように車を縦においてみましょう。もちろん、4輪ともブレーキで固定されているとします。
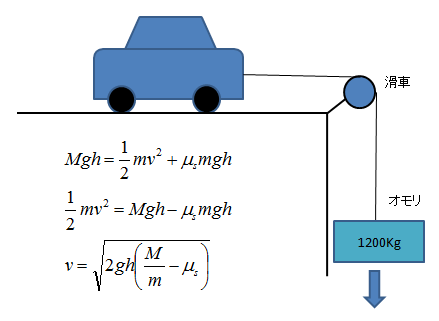
図2 縦方向に引っ張る例
さて、ここで問題となるのは、タイヤの縦方向の摩擦力と横方向の摩擦力の違いです。
今回は荷重は同じなので、摩擦係数の違いになりますね。
摩擦円は円なのか?に書いた通り、タイヤは縦方向の方が摩擦係数が大きく出来ています。
よって、横方向では摩擦係数を0.9としましたが、縦方向では仮に1.0としてみましょう。
すると、
F = 1.0×300×9.8 = 2940[N]
なので、
F = 2940×4 = 11760[N] = 1200[Kgf]
となりますね。
つまり、図の様に縦に車を置くと、1200Kg以上のオモリを付けると車が滑りだすことになります。
偶然?車体と同じ重さのオモリですね。
この、1200Kgという重さのオモリが引っ張る力が、この車のタイヤのグリップの限界と言う事になりますね。
タイヤのグリップは、4輪の合計でそれ以上のグリップを出すことは不可能、と言われていますね。(もちろん、空力によるダウンフォース等は無いとします。)
よって、例えば、もしも1300Kgのオモリを付ければタイヤが滑りだしますね。
そして、車はその場にとどまることができずに滑り続けて行くわけです。
タイヤのグリップより大きなグリップを出す事が出来ないと言う事は、これを止める手段は無いという事ですが、果たして本当に無いのでしょうか?
もしも自分がこの車に乗っていたとしましょう。車が後ろに引っ張られて滑り、崖に向かって行った時に、本能的にどうしますか??
恐らく多くの人は、アクセルを踏んで、ホイールスピンしてでも前に行こうとすると思います。
実はその本能は、当たっています。
ただ
この時に気を付けなければならないのは、滑り出したタイヤは、もはや最大摩擦係数である、静摩擦係数を出せないと言う事です。それは、動摩擦係数となり、静摩擦係数よりも小さな物となります。
それがいくつになるのかは、タイヤの種類や太さ、荷重など、色々な要素によって異なりますが、今回は仮に半分の0.5としましょうか。
それでは、まずオモリのする仕事を考えてみましょう。
今回は、オモリの重さをM、車体の重量をm、オモリの移動量をh、滑っている車の速度をv、重力をg、タイヤの動摩擦係数をμsとします。
自動車に必要な物理学より、仕事は、力×距離 でしたね。
今回は、1[m]引っ張られた状態での仕事を考えてみましょう。
オモリに掛かる力は、
F = M×g [N]
なので、仕事は、
U = M×g×h [J]
ですね。
この仕事、つまりエネルギーは、車の運動エネルギーとタイヤの摩擦エネルギーに対して行った物となりますね。
運動エネルギーは、1/2mv2で、
摩擦エネルギーは、μmgh ですね。
つまり、この系での仕事の式を作ると、
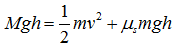
となりますね。
つまり、オモリが引っ張る仕事(エネルギー)は、車の運動エネルギーと、タイヤの摩擦エネルギーに変換されることになります。
そして
タイヤの摩擦エネルギーは、結果的に殆どが熱エネルギーに変換されることになります。
この時に、車の運動エネルギーと、車の滑る車速を求めてみると、上式より、
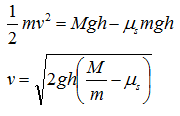
となりますね。
例えば、h=1[m]、とすると、
v=√2×9.8×1.0×(1300/1200-0.5)=3.38[m/s]
となりますね。
つまり、オモリが1[m]落下した時の車体の速度は3.38[m/s]となるわけですね。
フム。ここで驚くのは、vはhが大きいほど大きくなる、つまり滑る量が長くなるに従って速度が上がることになります。
つまり、車体は加速度運動をするわけですね。
こいつを微分してやれば加速度が出ますが、後述しますがμsは実は定数ではないので、ここではカットします。
さて、鋭い人はここである事を考えると思います。
それは、上式の速度vを0ににする事が出来たら、車体は滑らずにその場にとどまれるのではないか?と。
その方法こそが、ホイールスピンをさせてやると言う事です。
それではホイールスピンをさせるモデルについて考えてみましょう。
今回のモデルでは、4輪駆動とし、4輪の荷重は全て同じとします。
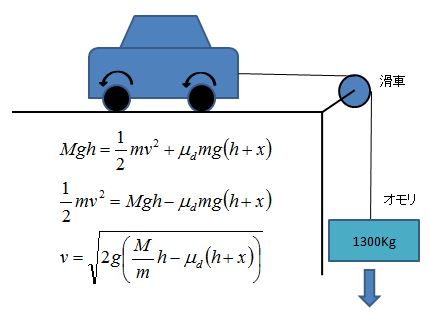
図3 ホイールスピンをして縦方向に引っ張る例
ホイールスピンをするモデルでは、仕事の式は、
![]()
となります。
ここで重要なのは、「タイヤは回転している」という事実です。
車が滑って1[m]移動させられるのと、タイヤがホイールスピンして1[m]分回転するのとでは、タイヤの摩擦エネルギーは同じとなるのです。
この式で、hはタイヤが静止している時と同じ車体が滑る距離、xはホイールスピンをした距離です。
先の例の
滑った距離に加えて、ホイールスピンをした距離の合計が、トータルのタイヤの滑った距離になります。
またμdは、ホイールスピン時の動摩擦係数です。これは、静摩擦係数よりも小さくなりましたね。
これより、滑る速度vを求めると、上式より、
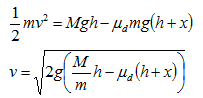
となりますね。式を整理しただけです。
速度を0にするには、
この式の右辺を0にできればいい事になります。
右辺を0にするには、ルートの中を0にすればいいわけで、
![]()
となればいいわけですね。
ここで、タイヤの滑る量は車体が停止している場合には、時間をt、タイヤの半径をr、タイヤの角速度、つまり回転数をωとすると、自動車に必要な物理学より、
x=2πrωt
となるので、式を書きかえると、
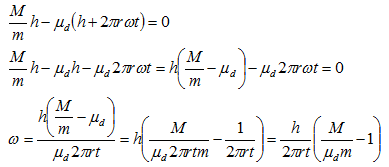
となりますね。
ちょっと難しいですか? ギリシャ文字を使っているだけで、中身は単なる中学数学です。
つまり、速度を0にするためのホイールスピンの回転数は、hとtとμdで決まる事になります。
hとtは、上記のタイヤが止まっているモデルの、車体が滑った距離h[m]と、滑るのにかかった時間t[s]から求まりますね。
要するに、ホイールスピンをしているモデルでは、外から見ているとオモリの位置は変わりませんが、相対的にオモリが落ちていると理解すればよいでしょう。
ちょっと概念が難しいかな?
さて、これで速度vが0となる様な、タイヤの回転数ωが求まります。
例えば、上記のタイヤが静止しているモデルで、h=1[m]で、t=1[s]、タイヤの半径r=0.1[m]、μd=0.5だったとすると、
ω=1/(2π×0.1×1)×{1300/(0.5×1200)-1}=1.85[rad/s]=106.39[度/s]
のホイールスピン回転数とすると、車は静止し動かなくなります。
と言う事は、、、上手くホイールスピンさせてやることで、タイヤの最大摩擦力、つまり最大グリップを超えたグリップ力を出すことができる事になります。
上手くとは、タイヤの動摩擦力μdとホイールスピンの回転数ωのバランスにより決まる事になります。
この事実は、コーナリングの仕方によっては、タイヤのグリップの限界を超えたコーナリング速度で曲がれる事を意味します。
私はこれを、「縦に曲げる」と呼んでいます。摩擦円が円でないことからも、縦グリップを使ったこの曲げ方は有効そうですね。
その技術については、ドラテク編に書く予定です。
ここで、μdやωをどれだけでも大きく出来る気がしますが、上式から面白い事が分かります。
hが0以上の値ならば、もしも、
![]()
となるような、μdやωとすると、ルートの中がマイナスになってしまうのです。
物理学では、虚数(複素数)の速度と言うのは定義されません。
よって、このような関係になることは有り得ないはずです。
と言う事わ、、、ω、つまりタイヤのホールスピン回転数を大きくすると、動摩擦係数μdが小さくなることになります。
よって、μdはホイールスピンの回転数によって変化する事になります。つまり定数ではないのです。
これは感覚的にも分かりますねぇ。「シャーッ」っと一気にホイールスピンをさせてしまうと、余計グリップが落ちそうですね。
よって、一番オモリに対抗する力が強いホイールのスピン回転数が、どこかに有るはずです。
残念ながら、その実験データは私は持っていませんが。
更に触れておくと、速度vが0ではなく、オモリを引っ張り上げてしまう場合。
その時には、上式のhとxの関係が逆方向なので、符号がマイナスになりますね。
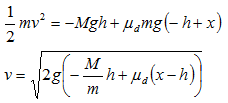
と言った感じですかね。
ただ、引っ張り上げる力が有ると言う事は、まだもっと重いオモリを付けられるという事になりますね。
この力は、実はコーナリングの立ち上がりで非常に有効な技術として使えるのですが、これもここでは触れない事にします。
そして、今回重要な事は静摩擦係数μsと動摩擦係数μdの差です。
上記の式より、この差が大きいタイヤでは、静止時に滑り出すような力が掛かった時に、ホイールスピンによるグリップ力を得るのが難しくなるし、逆に差が小さいタイヤでは得やすくなると言う事になりますね。
一般に、スリックタイヤなどでは差が大きく、ラジアルタイヤでは差が小さいようです。
さて、今回の話は、コーナリング時にタイヤを一切滑らさない方が速いのが、あるいは時によっては滑らせた方が速いのか、もっと俗に言うと、グリップと、ドリフトのどちらが速いのかと言う、昔からの論争?に対して、物理的な答えを示唆していると思います。
今回の答えから分かる事は、「適切にグリップ力を引き出せれば、タイヤを滑らせた方が速いこともある」、と言う事です。
その力の引き出し方は、またドラテク編かどこかに書く予定です。
さて、今回の話は面白かったですか??
タイヤの持っているグリップ力ってのは、実は思っているよりもずっと高い所にあるのです。
私はその領域の事を、「グリップの向こう側」と呼んでいます(笑)。
とりあえず、以上。