短く止めるブレーキングを考える（前編）

さて、止まるためのブレーキは、前項で「強くて短いブレーキ」が最良だとわかりましたね。

それでは次に、実際にどのようにブレーキペダルを踏んだら良いのか、どのように制動Gを立ち上げたら良いのかを、具体的に考えてみましょう。

ブレーキの踏み方については、ドラテク本や雑誌のドラテクコーナー、或いはプロが教えるドラテク講習でも良く出てきますね。
とりあえず、減速のためのブレーキ、止めるためのブレーキに限って言えば、みんな同じような事を書いていると思います。
恐らく、以下の様な図をどこでも見ると思います。

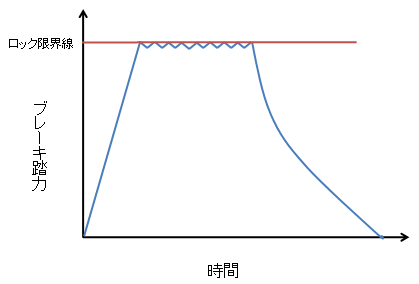
図1　時間とブレーキ踏力の図

とにかく、早く制動Gを立ち上げるようなブレーキの踏み方が重要で、初期から蹴っ飛ばす様に踏んで、ロックすれすれの一定のブレーキ踏力を維持する、と言う事ですね。
実際に多くの人が、この図をイメージしてブレーキを踏んでいると思います。
元々この図はデータロガーのグラフから来ているんだと思いますが、この図は、長年にわたりどこでも当たり前のように書かれていますね。恐らく誰も疑問を持たずに。

でも、本当に正しいのでしょうか？
もしもこの図よりも、最適なブレーキの踏み方が有れば、より短く止まれるので、当然速く走れるはずですね。
それでは、今回はその方法を考えてみましょうか。

その前に、今回はローターの温度変化などによるブレーキパッドのμ変化は無いとして、ブレーキの踏力、踏む力に比例してブレーキパッドとローターの摩擦力が決まるとします。
そう定義しないと、ちょっと計算が難しいので。

さて、図1で特徴的な所であり、私が一番気になったところは、ロック寸前の一番減速している時の、ブレーキ踏力が一定だと言う事です。
実際にロックラインは水平ですね。私はそれ以外の図や説明を見た事が有りません。

ブレーキングの話は実は結構難しく、運動エネルギーとブレーキが消費するエネルギーの話を理解する必要が有ります。
ただそれを理解してしまえば、誰よりも短時間で、短い距離で車を減速する事が出来るでしょう。
ちょっと難しいかもしれませんが、是非理解すると良いと思います。

今までにも書きましたが、ブレーキと言う装置は運動エネルギーを熱エネルギーに変換する事で、速度を落とす装置です。
と言う事で、運動エネルギーについてちょっとおさらいしてみましょう。
運動エネルギーは、1/2mv²でしたね？
今回は、計算の為に車重は1200Kgとします。

さて、この車を加速させるのに必要なエネルギーを考えてみましょう。
馬力と､トルクと、加速の関係に書いた通り、速度が上がれば上がるほど、同じ速度を上げるために多くのエネルギーが必要となりましたね。
それではちょっと、1200Kgの車を静止状態から、180Km/hまで加速する時に、5Km/h加速するために必要なエネルギーを書いてみましょう。
速度と、エネルギーの関係は下図の様になります。

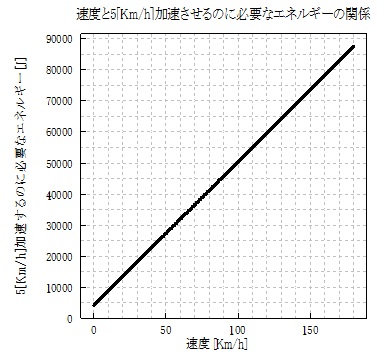
図2　速度と加速に必要なエネルギーの関係

このグラフの線は、2乗ではなく線形（1乗）すね。ちょっと意外かな？

さて、問題の減速は、これと全く逆のことをやる訳ですね。
5Km/h減速するためにブレーキが消費するエネルギーは、下図の様になりますね。
グラフの都合上、速度にマイナスが付いていますが、無視してください。

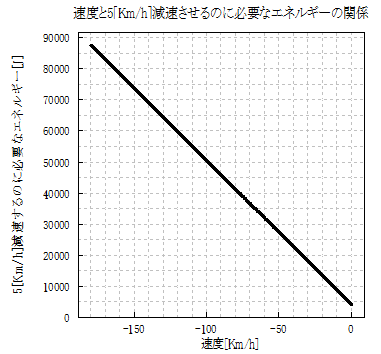
図3　速度と減速に必要なエネルギーの関係

つまり、高速域ほど同じ減速Gを出すためには、ブレーキは沢山のエネルギーを奪う必要が有る訳です。
何だか一見、同じ減速G（減速加速度）を保つためには、高速域ほどブレーキを強く踏む必要が有る気がしてきますねぇ。

しかしそれは間違いです。 パッドとローターの間の摩擦力が同じでも、高速域ほどローターが高回転で回るために、1秒当たりにパッドの中を通るローターの距離が多いのです。
例えば、50Km/hで走っている時と100Km/hで走っている時では、100Km/h時の方が倍の速さでローターが回転しているため、1秒当たり倍の距離通っている事になりますね。

エネルギー（仕事）とは、力×距離　でしたね？

つまり、同じ摩擦力でもローターが通る距離が倍なので、自動的に倍のエネルギーを奪ってくれるのです。
よって、同じ減速Gを保つためには、ブレーキ踏力は速度によって変わらない、と言う結果になります。

一応それをちゃんと証明するために、同じ減速Gを保つために必要なローターとブレーキパッドの摩擦力（これは踏力で決まる）をFとして、Fの式を作ってみましょうか。
高校物理で習った様に、加速度aで、t秒間に進む距離は、1/2at²なので、回転している状態から減速して回転数が0になるまでにパッドの中をローターが通る距離は、1/2at²ですね。

車重をm、速度をv、減速加速度（減速G)をa、時間をt、タイヤの半径をr₁、ローターの半径をr₂として、左辺をローターが奪うエネルギー、右辺を車が奪われる運動エネルギーとすると、

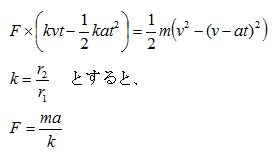
となりますね。ｔの項も速度vの項も消えてしまいましたね。
この式より、減速に必要なブレーキの踏力は、車重と出したい減速Gに比例し、ローターの半径に反比例する事が分かりますね。まあ、感覚通りかな？？

これより、車重mとタイヤの半径とローターの半径の比（上式のk）は変わらないので、ブレーキの踏力は減速G（上式のa）によってのみ決まり、減速Gが一定ならば、速度を問わずブレーキ踏力は一定で、図1が正しいと言う結論となりますね。

ちなみに、同じ減速Gを保つと書いていますが、何故これが重要かと言うと、車というのはブレーキロックする事が有るからです。ロックしてしまえば、タイヤと路面の摩擦係数が一気に落ちるので、制動距離は伸びますね。
このロックするかどうかが何で決まるかと言うと、減速Gです。
これは、速度によりません。 180Km/hだろうが、40Km/hだろうが、ロックする減速Gは同じです。
（細かく説明しませんが、簡単に言うとロックさせようとする力 F=ma で、mが車重、aが減速Gで、速度vの項は出てこないのでそうなりますね。）

このロック限界の減速Gは、何で決まるかと言うと、タイヤと路面の摩擦力ですね。
雪道や氷の上を走ると、これが小さくなるために、小さな減速Gでも簡単にロックしてしまうわけです。
よって、ロックしない程度に最大の減速Gを長く出し続けることが、短く止める最良の方法と言う事になりますね。
図1は正にそれを書いたものであり、ますます合っている気がしてきますね。
もしも車を止めるために、車の運動エネルギーだけを奪えば良いのだったら確かにこれは正しいでしょう。

しかしながら、ブレーキが止めなければならない物、奪わなければいけないエネルギーは、車の運動エネルギーだけでしょうか？
違いますね。
何度も書いた通り、車と言う機械は回転物の集まりです。
具体的には、フライホイールやミッションやクラッチ、ドライブシャフトにハブベアリング、そしてタイヤとホイール、更にブレーキローター自体も回転物ですね。

これらは、自動車に必要な物理学に書いたように全てイナーシャ、つまり慣性モーメントを持っています。
そして慣性モーメントを持っている物は、全て回転エネルギーを持っています。
ちょっと高校物理から外れますが、慣性モーメントをIとすると、
1/2Iω²
が回転エネルギーです。
つまり回転エネルギーは、回転数の2乗に比例する物なのです。

車のブレーキは、車の運動エネルギーだけでなく、これらの回転物全ての回転エネルギーを奪わなければなりません。
今回は、回転物の中でも特に重く、イナーシャが大きく止めにくい回転物として、タイヤとホイールを考えてみます。
イナーシャと言うのは、mr²でしたね？

つまり、イナーシャは質量が重ければ重い程、そしてその重量が回転軸から外に有ればある程大きくなる事になりますね。
重くて、その重量の殆どが回転軸の外寄りに有るもの…。 正に、タイヤとホイールがそうです。
最近のホイールの大インチ化や、タイヤの大径化は凄まじいですねぇ。
17インチや18インチの車が、普通に売られていますから。中には、Z34やR35GT-Rの様に、標準で19インチや20インチの物まで有りますね。
まあ、今までの話を読んで来ている人は理解していると思いますが、イナーシャと言うのは質量よりも、回転軸からの距離が重要です。
mr²より、イナーシャは質量に対しては1乗ですが、距離の2乗で大きくなるので当然ですね。
つまり、質量が2倍になってもイナーシャは2倍ですが、質量が同じでも、回転軸からの距離が2倍になると、イナーシャは4倍になる事になります。距離が3倍なら、9倍ですね。

更に、ホイールの重量はどこが一番重いでしょうか？ホイールナットの辺りでしょうか？スポークでしょうか？リム部でしょうか。
まあ、見るからにリム部が容積が大きくて、重そうですねぇ。
さらにタイヤは？？
タイヤなんて、ホイールよりもさらに外に付いていますね。
特に、扁平率の低い薄いタイヤだと、殆どが回転軸から一番遠い所にその質量が有りそうですね。

つまりこれらのホイールの大インチ化やタイヤの大径化、扁平率の低化は、実はイナーシャを大きくして、加速も減速もしにくくしている訳です。
例え重量が同じでもです！！

更に、物理法則には、角運動量保存則と言う非常に重要な物が有り、これは回転物には、回転軸の方向を一定に保とうとする力が働くという物です（コマが回っていると倒れないのはこの力のおかげ）。
この力もイナーシャが大きくなる程大きくなるので、タイヤが向きを変えにくくなる、つまり曲がりにくくなる訳です。

つまり簡単に言うと、たとえ重量が同じでも、インチアップすればするほど、止まらない、加速しない、曲がらない、と言った具合に、運動性能が低下する訳です。
まあ、この話はまたどこか詳しくに書くつもりです。

おっと。ちょっと長くなったので、、、後編へ続く…。

Back Top