ホイールスピンさせると本当にグリップを超えた力が出るのか？

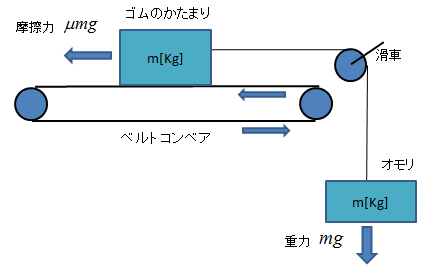
えー、前回説明したベルトコンベアのモデルですが、ちょっと例が悪かったですね。
更に途中から説明が間違っていました。失礼しました。

高校までの物理では、動摩擦係数μはどんな条件でも一切変化しません。
つまり摩擦力は、ゴムと路面が滑るスピードが時速1Kmだろうが、時速300Kmだろうが同じ、と言う事です。
もちろん、現実の世界ではそんな事は有りませんが、高校物理ではそう習います。

前回のベルトコンベアの説明は、ゴムとベルトコンベアの間の「滑り量（単位時間に滑る距離）」がベルトコンベアを動かしても止めても変化しないと言う条件でしか成り立ちませんでした。
しかしベルトコンベアを加速させると、ゴム（とオモリ）には慣性が有るので、滑っているゴムはより滑り量が増しますね。
結果、ゴムの動きは変わらない事になります。
これはあまり良くない間違いだったので、訂正しておきます。

あと大分前に書いた記事ですが、タイヤのグリップを超えたグリップ力を出すに書いたのも同様で、初期の方の方程式から間違っています。 どこが違うかわかるかな？？（笑）
 一応ヒントを書いておくと、「オモリの運動エネルギーとエンジンの仕事（エネルギー）」です。

あっちの方は、学習用に敢えてそのまま残しておくので、自分でどこが違うのか考えてみて下さいね。



しかし実際に、ホイールスピンをさせる事で滑っていない時よりも大きな摩擦力が出るのは本当です。
その一つの理由は、タイヤは滑らせた方がグリップするに書いた様なタイヤの特性からです。

ただこれは、少なくとも高校物理からは、はみ出してしまいます。
また、μ特性の変化を理論的にビシッと表す様な数式もどうやらない様です。　
恐らくこれらの結果は全て、実験から出された物でしょう。 タイヤは滑らせた方がグリップするに描かれたグラフも、実験値を最小二乗フィットとかをした物だと思います（この辺の話は難しいので無視してもいいです）。

よって、なぜそうなるのかをここで考察するのは止めておきます。

詳しく知りたい人は、「タイヤ、摩擦力、スリップ率」、といったキーワードで検索するとタイヤの滑り量と摩擦の関係の論文などが、いくつか出てくるのでそっちを見てみて下さい。 （ABS等のブレーキ系の論文が多いようですが）
難しい話がキライって言う人は、特に読まなくてもいいでしょう。 とにかく実験すると結果はそうなるって感じです。

そして訂正の代わりにもう一つ、私の考えるホイールスピンさせる事で大きな遠心力に対抗する力が出せる理由を簡単に書いておきます。

円運動をする物体に遠心力が働くのは、いいですね？ 知らない人は自動車に必要な物理学 を読んでくださいね。
それに対して遠心力とは逆の方向、円の中心の方向に「向心力」が働いているのもいいですかね？
これは、自動車に必要な物理学 には書かなかったですが、高校物理で習う物です。

例えば糸の先にオモリを付けてクルクル回してもオモリが遠心力で外側にすっ飛んで行かないのは、糸が中心の方向に遠心力と同じ力で引っ張っているからです。この糸の引っ張る力のことを向心力と言います。
スペースシャトルや人工衛星が落っこちてこないのも、地球の重力による向心力が遠心力と釣り合っているからです。

そして遠心力は、当然コーナリング中の車にも働いています。
そしてコーナリング中の車にももちろん向心力が働いています。　それが、タイヤの摩擦力です。
通常は向心力となるのは、タイヤの横グリップですね。
その向心力として、より大きなタイヤのグリップ（摩擦力）を出すために考えたのが、タイヤの縦の摩擦力を使う事です。
これは、グリップの向こう側（理論編）に書いてあるので詳しくはそっちを見て下さい。

ここで非常に重要な事を一つ書きます。
それは、「タイヤの横グリップは、遠心力よりも大きい向心力を出せない」、と言う事です。

なぜなら横グリップは摩擦力ですから、引っ張られて始めて発生する力です。
これはいいですね？　机の上に置いた消しゴムを引っ張れば、引っ張った方向と逆方向に摩擦力が発生しますよね？
しかし置いてある消しゴムに急に摩擦力が発生して、動きだしたりしませんね？
また糸で引っ張ったら、引っ張る力よりも強い摩擦力が発生して、糸を引き戻したりする事も有りませんね？
例えば摩擦係数がμだとすると計算上は摩擦力はμmgになりますが、実際には最低でもμmgと同じか、それ以上の力で引っ張ってやらなければその摩擦力は発生しないのです。

摩擦力とはそういう少し変わり者の力なのです。
では、引っ張った力が小さくても、この最大の摩擦力を出す方法は無いのでしょうか？

そこで考えたのが、タイヤを縦に滑らせると言う話になるのです。
何故なら、タイヤをホイールスピンさせてやることで、引っ張った力よりも大きな力を発生させる事が出来るのからです。
つまり、遠心力によって生じるタイヤの向心力＝グリップ力、よりも大きな力を発生できる訳です。
乱暴に言えば、タイヤが引きずられて始めて出る大きな摩擦力を、引きずられなくても出せるのです。

これは 極端な話、車が例えその場に静止していても、タイヤが大きな摩擦力を発生できるのです！
ここが置いてある消しゴムが、単体で摩擦力を発生しないのとは違う所です。

ガチで速くなる練習方法の方に後々ゆっくりと理論を書く予定ですが、車の性能を最大限に出すには、究極的に言えば、常にタイヤにこのμmgの摩擦力を発生させる事です。
加速時、減速時、コーナリング時、の全ての場面においてです。

具体的には、最大の摩擦力を使ったホイールスピンギリギリの加速に、最大の摩擦力を使ったロックすれすれのブレーキング。そして滑るすれすれのコーナリング。
逆にこれ以上の加速Gや減速Gや、横Gを出す事は不可能な訳です。

ホイールスピンギリギリの加速に、ロックすれすれのブレーキングについては誰も異論は無いでしょう。 これ以上の加減速は、基本的には無いでしょう。
ただコーナリングについては、まだ詰める方法が有るのです。
それがこの、タイヤの縦方向の摩擦力を使う方法です。
ホイールスピンさせるのは、コーナリング中に縦方向のタイヤの回転を止める事は不可能だからです。 （仮にタイヤに力（駆動力）を与えなければ、理論上は遠心力によって逆回転してしまうはずです。）
ただ結果的にはタイヤは滑らせた方がグリップするより、タイヤを停止させるよりもホイールスピンさせた方が大きな摩擦力を発生出来るので、より良い訳です。

もちろん、遠心力よりも大きな向心力を発生させれば、車はより小さく曲がろうとするでしょう。 正確に言えば、より小さな半径の円を描くようになるはずです。
そうすればスピードが同じでも、F=mv²/rより、遠心力は増していき、最終的に遠心力は摩擦力と同じ力になるでしょう。
そうなるとあまり意味が無いと思うかな？？
でも実は、これがとても重要な事なのです。
まあ、この話はガチで速くなる練習方法の方に分かりやすく書く予定ですので、今回はこの辺にしておきます。


今回は時間が無かったんで 急いで書いたからちょっと難しかったですかね？
そのうちに分かりやすいモデルと説明を考えて、改めて書く予定です。
この話はもう少し時間下さい（笑）。

取りあえず今回は、訂正まで…。


Back        Top