サイン波と矩形波　その２

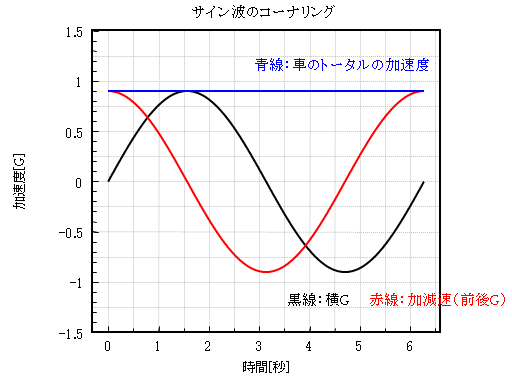
図4　サイン波コーナリングのイメージ


さて、続きです。

まずサイン波運転ですが、フルブレーキ時はいいですね？これは確かに0.9[G]に近い数字が出るでしょう。 ですがブレーキの話に書いた通り、最大の減速Gを出すにはフルブレーキング時に前後のタイヤに掛かる荷重が出来る限り同じである必要があるでしょう。 そしてポルシェなどのリアエンジンの車はそのために有利なレイアウトでしたね？？
さて、問題はコーナリングです。 1.5秒までブレーキを緩めながら、つまりブレーキを残してハンドルを切るとタイヤに掛かる荷重はどうなるでしょう？
当然ながらブレーキを踏んで減速Gが出ていれば、前輪の荷重が後輪よりも大きいことになります。 FF車などの前にエンジンのある車ならば、静止時でさえ前輪の荷重が大きいので、減速時には荷重の殆どが前輪に乗っているでしょう。
ここで思い出して下さい。 タイヤの荷重とグリップの非線形性の話を。 タイヤを太くすると何故グリップが上がるのかや、車重と荷重とグリップの関係を見ればわかる通り、前輪だけに大きい荷重を乗せると、タイヤの摩擦係数がだんだんと落ちていってしまいます。 つまり本来は0.9であったはずの摩擦係数が、例えば0.7とかになってしまうわけです。
車が発生する最大の摩擦力、つまりグリップ力は、

F＝μmg

でしたね？　ここでmは車重、gは重力加速度です。
これは4輪に均等に荷重が掛かっている時に発生できる理想値です。 ところが荷重が前輪だけに乗ってしまうとμの値が下がってしまうのです。 そうなると車全体のグリップが下がることになりますね。
それを防ぐために、大きな荷重が掛かる重い車では太いタイヤを履いて接地面積を増やしたり、レーシングカーでは荷重移動を減らすために足を固めたり重心を下げてロールやピッチングを減らしているわけです。
μを落とさずに維持し続けるためには、つまりタイヤの性能を最大に出すためには、出来る限り4輪に均等に荷重を掛ける必用があるわけです。

その観点から言うと、1.5秒までブレーキを残している運転はどうでしょうか？
これではコーナリングを始めてから1.5秒間、クリップまでずっと前輪に大きな荷重が乗っていて、後輪には殆ど荷重が掛かっていません。 この間は車全体のμが最大になるような、4輪に均等な荷重を掛けられていないわけです。
つまりクリップまでの1.5秒間は、タイヤのμは0.9をずっと下回っていることになります。 図4では加減速Gと横Gを足した青線は常に一定で0.9となっていますが、実際にはそうはなりません。 青線は0.9を殆どの域で下回っていることになります。

更に加速と共に横Gが減っていくクリップから先の区間でも、サイン波運転はあまり良いとはいえません。
フロントが重く、且つ4輪駆動の車ならばこの運転でもデメリットはあまりないでしょう。 フロントが重ければ 加速時に4輪にほぼ均等に荷重がかかるし、全てのタイヤが駆動しているので横グリップも全てのタイヤで同じでしょう。
では例えばリアエンジンの後輪駆動車の場合はどうなるでしょうか？
まず加速すれば荷重の殆どは後輪に掛かります。 更に後輪に駆動力が掛かるので、摩擦円の理論より後輪の横グリップは減ることになります。 そうなると荷重移動によって車全体の発生できる限界のGが落ちる上に、駆動力によって後輪だけが横グリップが減ることになります。 恐らくリアが先に限界を超えて滑るオーバーステアのようなアンダーステアが出るでしょう。
（逆にフロントタイヤは殆ど仕事をしていない（力を発生していない）でしょう）

それを防ぐためにリアエンジンの後輪駆動車は、普通はリアタイヤの方がかなり太くなっているはずです。 それでも加減速が全くない場合に比べると、耐えられる遠心力は小さくなるはずです。
つまりクリップから先の旋回加速時においては、二輪駆動車の場合は駆動していないタイヤに大きな横Gに対向する力を発生させる必要が出てきそうですね。 駆動輪の横グリップは落ちているわけですから。 しかしながらこれを運転やセッティングで行うのはとても困難でしょう。
よって通常は、2輪駆動車では恐らく1.5秒から先の加速区間においても、加速Gと横Gを足した青線は0.9[G]を大きく下回っているでしょう。

これらの理由により、私はサイン波運転は最適値からは遠いと考えています。

ちなみにカートではその構造上ブレーキを残してコーナーに入るし、フォーミュラカーの様な空力によるダウンフォースが大きいレーシングカーでは、クリップから加速すると共に強烈なダウンフォースが掛かってタイヤのグリップが上がるために上記の現象が当てはまりにくいのかもしれません。
そのためカートやフォーミュラカー出身のドライバーの中には、この様なサイン波運転の答えに行き着く人が居るのではないかと思っています。
逆にハコ車が得意なドライバーやラリードライバーは、このような運転をしない傾向にあるように見えます。
（例えばこのHPにも何度も登場しているガンさん事、黒沢元治氏は「ブレーキは残さない」と言っていました）
更に余談ですが欧州のドライバーの間では、ブレーキを残す「サイン波運転」はメジャーではないようです。
この運転は日本独特のものなのかもしれませんね。


さて、そこで矩形波運転の登場です。 この運転はサイン波運転の問題点をかなり解決します。


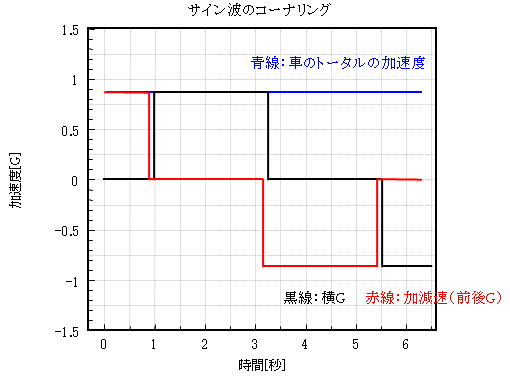
図5　矩形波コーナリングのイメージ

まず矩形波運転では、ブレーキによる減速とコーナリングがオーバーラップしません。
よってブレーキは減速だけ、コーナリングは曲がるだけの力を発生するため、旋回ブレーキや旋回加速がありません。
それではこの運転も、図5の時系列で見て行きましょうか。

まず始めにブレーキングですね。 フルブレーキ時にほぼ0.9[G]を発生するのはサイン波運転と同じです。 これ以上の減速Gは発生できないので、制動はこれが最適値でしょう。
次に1秒辺りでコーナリングが始まりますが、この時にブレーキは完全に抜いています。つまり前後方向の加速Gは有りません。よってタイヤはいきなり最大の横Gを発生できることになります。 そしてこの運転では旋回中の加減速がないために、前後方向の荷重移動は有りません。 荷重バランスは静止時と同じです。 そうなると荷重とグリップの非線形性は無視出来ます。
よってこの運転ではタイヤの摩擦係数は常に0.9になるので、常に完全に0.9[G]を発生できることになります。 理想値の青い線は、そのまま実際の値になるでしょう。
更にクリップを過ぎても旋回中は加速しないため、コーナーが終わるまでの間は常にタイヤは最大のグリップである0.9[G]を発生していますね？
コーナーが終われば今度は横Gが無くなるため、全てのグリップを加速に使えることになります。
これが矩形波運転の基本です。 これはとにかく出来るだけ長い区間で、タイヤが出せる理論上の最大Gである0.9[G]を出す運転です。 私はこれが最も速い運転、最適値だと考えています。

この矩形波運転をすることが、「ガチで速くなる練習方法」の最終目的です。
矩形波運転ではコーナリング中にハンドルを動かすことはないですよね？
コーナリング中のアクセル操作は、最大の遠心力に対向する操作に書いたバランススロットルになるのが理想です。
つまり加減速を一切しない、定速にするためのアクセルです。
そして定速で同じRを描くのであれば、ハンドルの舵角は一定になるはずですね？
加減速もなく、横Gの変化もなければ、車の限界を下げてしまう荷重変動も一切ないはずです。
これがブレーキを残すサイン波運転のステアリング操作とは違う点です。

「ガチで速くなる練習方法」には、ハンドルの舵角を出来る限り小さい舵角で一定にして、そして出来る限り長い間その舵角を切っているようにと書きましたね？
そう意識すると、必然的にこの矩形波運転になるはずです。
そして久しぶりの資料映像に、「上手く決まるとハンドルを戻すスピードが速くなる」と書きましたが、それもこの矩形波運転となれば当然ですね。
また「コーナリング中の舵角一定運転は、定速で行うのが理想」と書いたのも、この矩形波運転を目指すためです。
たとえタイヤのグリップ限界よりもずっと手前のGで走っていても、この運転ならば荷重変動はないはずですし、タイヤに掛かる負担も4輪が均等な上に、入口から出口まで常に同じはずです。
結果的にタイヤにも優しく、燃費も良く、乗り心地も良くなるでしょう。

ちなみにこの運転もデータロガーで加速度を測定してグラフを見ると、実際にこの様に矩形波の形になっています。


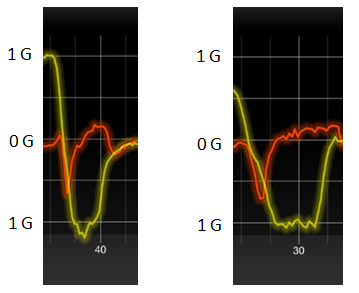
図6　サイン波形状のデータと矩形波形状のデータ

これは実際に加速度センサーを使った簡易的なデータロガーで、私の運転を記録したグラフです。
黄色い線が横Gで、赤い線が前後Gです。 赤い線は０[G]より下が減速Gで、上が加速Gです。
左のグラフがサイン波運転の例です。 赤い線のブレーキが弱まるに連れて黄色い横Gが強まっていくのがわかると思います。
そして横Gが最大になる瞬間は、見事に赤い線が０をまたぐ瞬間ですね。そして加速とともにまた横Gが減って行くのがわかります。
これを見ると摩擦円の理論ってのは本当に正しいんだなぁ、と思いますね。
次に右が矩形波運転の例です。あまり綺麗な矩形波ではありませんが、左と比べると減速Gと横Gのオーバーラップが少なく、減速Gと横Gがくっきりと分かれていると思います。 また横Gが一定でコーナリング中は加減速の変化が少ないのがわかると思います。


さて、この矩形波運転ですが、これは理想値ですが実際にやるのは非常に困難なはずです。 なぜならラインも運転の操作も、あまりにピンポイントの運転になるからです。
サイン波運転が途中である程度修正できるのに比べて、矩形波運転はオーバーラップが殆ど無いために色々な操作がとてもシビアになります。
ですからこれはあくまで理想値で、それにできるだけ近づける事を目的とするものです。

例えばコーナリング速度は、横Gがキッチリ0.9[G]になる速度での進入が理想ですが、なかなかそれ程ピッタリの速度でコーナには入れません。 ですから実際にはやはり、スローイン・ファストアウトに近い運転になるでしょう。
つまり矩形波運転では旋回加速はしないと書きましたが、進入スピードは少しマージンを取るために実際にはコーナーの途中で加速をするケースが多くなるでしょう。
またパワーの低い、加速力の低い車と、加速力の高い車とでは加速時のラインや操作が異なることもあります。
そしてオーバラップもゼロにすることは不可能でしょう。
それでも出来るだけ矩形波に近づける事が目標なのです。

また矩形波運転は、仮に進入スピードがピッタリでも車に正しいヨーがついていなければ曲がることが出来ません。
そうなるとあるレベル以上ではどうしても、「本気で速くなりたい人へ・・・」に書いた、荷重曲げの技術も必要となって来るでしょう。 更に今回は詳しくは書きませんが、これにトラクションステア効果を加えればもうワンランク上のスピードで曲がれる、非常に強力な武器となります。（決まればトラクションステア効果を出していても舵角は一定となります）
この運転は今までに練習してきたことの、集大成と言えるでしょう。

えー、ちょっと難しい話が続いたので、実際の矩形波運転の資料映像でも載せておきます。
興味のある方はこちらから見て下さい。


と、、、「ガチで速くなる練習方法」の根底にある理論は大体こんな感じです。
それではまあこんな話も参考にしつつ、色々考えながら練習してみて下さいね。

以上


Back        Top